
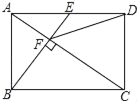
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .其中正确的结论有( )
.其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】A
【解析】
①正确.只要证明∠EAC=∠ACB,∠ABC=∠AFE=90°即可;
②正确.由AD∥BC,推出△AEF∽△CBF,推出![]() =
=![]() ,由AE=
,由AE=![]() AD=
AD=![]() BC,推出
BC,推出![]() =
=![]() ,即CF=2AF;
,即CF=2AF;
③正确.只要证明DM垂直平分CF,即可证明;
④正确.设AE=a,AB=b,则AD=2a,由△BAE∽△ADC,有 ![]() =
=![]() ,即b=
,即b=![]() a,可得tan∠CAD=
a,可得tan∠CAD=![]() =
=![]() =
=![]() .
.
如图,过D作DM∥BE交AC于N.
∵四边形ABCD是矩形,∴AD∥BC,∠ABC=90°,AD=BC,∴∠EAC=∠ACB.
∵BE⊥AC于点F,∴∠ABC=∠AFE=90°,∴△AEF∽△CAB,故①正确;
∵AD∥BC,∴△AEF∽△CBF,∴![]() =
=![]() .
.
∵AE=![]() AD=
AD=![]() BC,∴
BC,∴![]() =
=![]() ,∴CF=2AF,故②正确;
,∴CF=2AF,故②正确;
∵DE∥BM,BE∥DM,∴四边形BMDE是平行四边形,∴BM=DE=![]() BC,∴BM=CM,∴CN=NF.
BC,∴BM=CM,∴CN=NF.
∵BE⊥AC于点F,DM∥BE,∴DN⊥CF,∴DM垂直平分CF,∴DF=DC,故③正确;
设AE=a,AB=b,则AD=2a,由△BAE∽△ADC,有 ![]() =
=![]() ,即b=
,即b=![]() a,∴tan∠CAD=
a,∴tan∠CAD=![]() =
=![]() =
=![]() .故④正确.
.故④正确.
故选A.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共50棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树的总金额为56000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;
(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
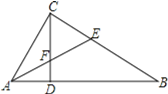
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线分别交BC、CD于E、F.
(1)求证:∠ACD=∠B
(2)求证:△CEF是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
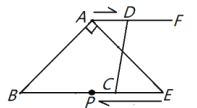
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 且点
且点![]() 在点
在点![]() 的右侧.点
的右侧.点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 方向以
方向以![]() /秒的速度运动,同时点
/秒的速度运动,同时点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 方向以
方向以![]() /秒的速度运动,在线段
/秒的速度运动,在线段![]() 上取点
上取点![]() ,使得
,使得![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒.当
秒.当![]() __________秒时,以
__________秒时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买![]() 种图书花费了3000元,购买
种图书花费了3000元,购买![]() 种图书花费了1600元,A种图书的单价是
种图书花费了1600元,A种图书的单价是![]() 种图书的1.5倍,购买
种图书的1.5倍,购买![]() 种图书的数量比
种图书的数量比![]() 种图书多20本.
种图书多20本.
(1)求![]() 和
和![]() 两种图书的单价;
两种图书的单价;
(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了![]() 种图书20本和
种图书20本和![]() 种图书25本,共花费多少元?
种图书25本,共花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了![]() ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
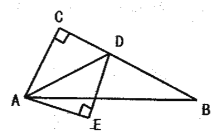
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的动点,连接
边上的动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的下方作等腰直角三角形
的下方作等腰直角三角形![]() .
.
(1)填空:![]() 的面积等于 ;
的面积等于 ;
(2)连接![]() ,求证:
,求证:![]() 是
是![]() 的平分线;
的平分线;
(3)点![]() 在
在![]() 边上,且
边上,且![]() , 当
, 当![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止时,求点
停止时,求点![]() 相应的运动路程.
相应的运动路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com