
分析 (1)将(0,1)代入得:4a+c=1,然后将4a+c=1与2a+c=0联立可求得a、c的值;
(2)将a=$\frac{1}{2}$,c=-1代入得y1=$\frac{1}{2}$(x-2)2-1,抛物线的对称轴为x=2,然后在-2≤x≤1范围内,当x=-2时,y1有大值,当x=1时,y1有最小值;
(3)由题意可知y2=$\frac{1}{2}$x2-(k+2)x+1,抛物线的对称轴为x=k+2,然后分为k+2<-2、-2≤k+2≤1、k+2>1三种情况分别求得y2的最小值即可;
(4)由g(k)=1列出关于k的方程,从而可求得k的值.
解答 解:(1)将(0,1)代入得:4a+c=1.
又∵2a+c=0,
∴2a=1,解得:a=$\frac{1}{2}$.
∴c=-2a=-2×$\frac{1}{2}$=-1.
(2)∵a=$\frac{1}{2}$,c=-1,
∴y1=$\frac{1}{2}$(x-2)2-1.
∴x=-$\frac{b}{2a}$=2.
∵x=2不在-2≤x≤1之内,
∴当x=-2时,y1有最大值,最大值为=$\frac{1}{2}$×16-1=7,当x=1时,y1有最小值,最小值为=$\frac{1}{2}$×1-1=-$\frac{1}{2}$.
(3)∵y2=y1-kx,
∴y2=$\frac{1}{2}$(x-2)2-1=-kx=$\frac{1}{2}$x2-(k+2)x+1.
∴抛物线的对称轴为x=k+2.
当k+2<-2时,即k<-4时,当x=-2时,y2有最小值,y2的最小值=$\frac{1}{2}$×4+2(k+2)+1=2k+7;
当-2≤k+2≤1时,即-4≤k≤-1时,当x=k+2时,y2有最小值,y2的最小值=$\frac{1}{2}$(k+2)2-(k+2)2+1=-$\frac{1}{2}$(k+2)2+1.
当k+2>1时,即k>-1时,当x=1时,y2有最小值,y2的最小值=$\frac{1}{2}$×1-(k+2)+1=-k-$\frac{1}{2}$.
综上所述,g(k)的解析式为g(k)=$\left\{\begin{array}{l}{2k+7(k<-4)}\\{-\frac{1}{2}(k+2)^{2}+1(-4≤k≤-1)}\\{-k-\frac{1}{2}(k>-1)}\end{array}\right.$.
(4)当k<-4时:令y=2k+7=1,得k=-3,不合题意舍去;
当-4≤k≤-1时:令y=-$\frac{1}{2}$(k+2)2+1=1;得k=-2.
当k>-1时:令y=-k-$\frac{1}{2}$=1,得k=-$\frac{3}{2}$,舍去.
综上所述,k=-2.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、二次函数的性质,找出二次函数在自变量取值范围内取得最小值的条件是解答本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
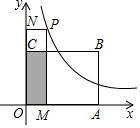 如图,矩形OABC的四个顶点分别为O(0,0),A(2,0),B(2,1),C(0,1),P(x,y)是反比例函数y=$\frac{1}{x}$(x>0)图象上的一个动点,过点P作PM⊥x轴,PN⊥y轴,M、N为垂足,记矩形OMPN与矩形OABC的重叠部分面积为S,则S与x轴的函数关系式的图象为( )
如图,矩形OABC的四个顶点分别为O(0,0),A(2,0),B(2,1),C(0,1),P(x,y)是反比例函数y=$\frac{1}{x}$(x>0)图象上的一个动点,过点P作PM⊥x轴,PN⊥y轴,M、N为垂足,记矩形OMPN与矩形OABC的重叠部分面积为S,则S与x轴的函数关系式的图象为( )| A. | 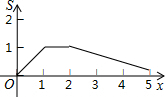 | B. | 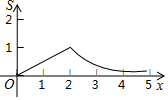 | ||
| C. | 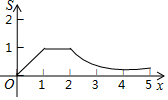 | D. | 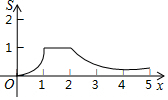 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
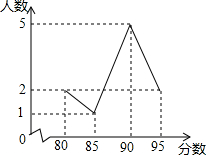 在学校演讲比赛中,10名选手的成绩折线统计图如图所示,则下列说法正确的是( )
在学校演讲比赛中,10名选手的成绩折线统计图如图所示,则下列说法正确的是( )| A. | 最高分90 | B. | 众数是5 | C. | 中位数是90 | D. | 平均分为87.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
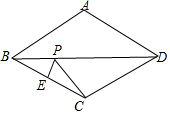 如图,在菱形ABCD中,∠ABC=60°,AB=1,E为BC的中点,则对角线BD上的动点P到E、C两点的距离之和的最小值为( )
如图,在菱形ABCD中,∠ABC=60°,AB=1,E为BC的中点,则对角线BD上的动点P到E、C两点的距离之和的最小值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 人数 | 3 | 4 | 2 | 1 |
| 答对题数 | 4 | 5 | 7 | 8 |
| A. | 4和5 | B. | 5和4 | C. | 5和5 | D. | 6和5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
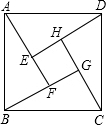 如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( )
如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{2\sqrt{13}}}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,以AC为直径的⊙O与边AB、BC分别交于点D、E.过E的直线与⊙O相切,与AC的延长线交于点G,与AB交于点F.
如图,△ABC中,AB=AC,以AC为直径的⊙O与边AB、BC分别交于点D、E.过E的直线与⊙O相切,与AC的延长线交于点G,与AB交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com