
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:填空题
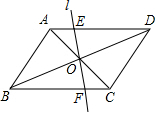 在?ABCD中,AB=6,BC=8,∠ABC=60°,AC、BC交于点O,过点O作任意l交AD于点E,交BC于点F(除端点外),则四边形ABFE周长的最小值为14+3$\sqrt{3}$.
在?ABCD中,AB=6,BC=8,∠ABC=60°,AC、BC交于点O,过点O作任意l交AD于点E,交BC于点F(除端点外),则四边形ABFE周长的最小值为14+3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
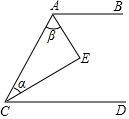 请将下列证明过程补充完整:
请将下列证明过程补充完整:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),现把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(1,-1).
如图,在平面直角坐标系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),现把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com