
����Ŀ����ͼ����ֱ֪��lAC��y=��![]() ��x�ᡢy��ֱ�ΪA��C���㣬ֱ��BC��AC��x���ڵ�B��
��x�ᡢy��ֱ�ΪA��C���㣬ֱ��BC��AC��x���ڵ�B��
��1�����B�����꼰ֱ��BC�Ľ���ʽ��
��2������OBC����BC�߷��ۣ��õ���O��BC������O����ֱ��O��E��ֱx���ڵ�E��F��y����һ�㣬P��ֱ��O��E������һ�㣬P��Q�������x��Գƣ���|PA��PC|���ʱ�������QF+![]() FC����Сֵ��
FC����Сֵ��
��3����M��ֱ��O��E��һ�㣬��QM=3![]() ���ڣ�2���������£���ƽ��ֱ������ϵ�У��Ƿ���ڵ�N��ʹ����Q��F��M��N�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵�����ɣ�
���ڣ�2���������£���ƽ��ֱ������ϵ�У��Ƿ���ڵ�N��ʹ����Q��F��M��N�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��B��6��0����y=![]() x��2
x��2![]() ����2��5
����2��5![]() ����3����6��3
����3����6��3![]() ����0��
����0��![]() ����0��7
����0��7![]() ������6��9
������6��9![]() ��.
��.
��������
��1�����ô���ϵ�������A��C�������꣬�ٸ�����ֱ�ߴ�ֱk�ij˻�Ϊ-1�����ֱ��BC�Ľ���ʽ���ɽ�����⣻
��2������֤����ACO=30�㣬��ͼ����QH��AC��H����y����F����FH=![]() CF�����ݴ��߶���̿�֪��QF+
CF�����ݴ��߶���̿�֪��QF+![]() FC����СֵΪ�߶�HQ�ij���
FC����СֵΪ�߶�HQ�ij���
��3�������M������������ηֱ�������⼴��.
�⣺��1��������A����2��0����C��0����2![]() ����
����
��ֱ��lAC��y=��![]() ��BC��AC��
��BC��AC��
��ֱ��BC�Ľ���ʽΪy=![]() x��2
x��2![]() ��
��
��y=0�����x=6��
��B��6��0����
��2���ߡ�OBC����BC�߷��ۣ��õ���O��BC��
��ɵ�O�䣨3����3![]() ����
����
��|PA��PC|���ʱ����P��ֱ��AC�ϣ���ʱP��3����5![]() ����
����
��P��Q����x��Գƣ�
��Q��3��5![]() ����
����
��Rt��AOC����tan��ACO=![]() =
=![]() ��
��
���ACO=30�㣬
��ͼ����QH��AC��H����y����F��
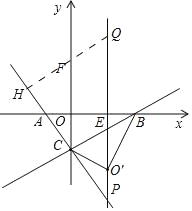
��FH=![]() CF��
CF��
���ݴ��߶���̿�֪��QF+![]() FC����СֵΪ�߶�HQ�ij���
FC����СֵΪ�߶�HQ�ij���
��Rt��PQH�У��ߡ�HPQ=��ACO=30�㣬PQ=10![]() ��
��
��HQ=![]() PQ=5
PQ=5![]() ��
��
��QF+![]() FC����СֵΪ5
FC����СֵΪ5![]() ��
��
��3���ɣ�2����֪��F��0��4![]() ����
����
��QM=3![]() ��
��
��M��3��2![]() ����3��8
����3��8![]() ����
����
��M��3��2![]() ��ʱ����ͼ����Q��F��M��N�ĵ�Ϊ������ı�����ƽ���ı��Σ��ɵ����������ĵ�N����Ϊ��6��3
��ʱ����ͼ����Q��F��M��N�ĵ�Ϊ������ı�����ƽ���ı��Σ��ɵ����������ĵ�N����Ϊ��6��3![]() ����0��
����0��![]() ����0��7
����0��7![]() ��,
��,
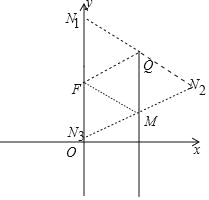
��MΪ��3��8![]() ��ʱ��ͬ���ɵ����������ĵ�N����Ϊ��6��9
��ʱ��ͬ���ɵ����������ĵ�N����Ϊ��6��9![]() ����0��7
����0��7![]() ����0��
����0��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB��CD�Ĺ�������BD=![]() AB=
AB= ![]() CD���߶�AB��CD���е�E��F֮�������10cm����AB��CD�ij���
CD���߶�AB��CD���е�E��F֮�������10cm����AB��CD�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=![]() x����A1����Ϊ��1��0��������A1��x��Ĵ��߽�ֱ���ڵ�B1����ԭ��OΪԲ�ģ�OB1��Ϊ�뾶������x���ڵ�A2���ٹ���A2��x��Ĵ��߽�ֱ���ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������x���ڵ�A3��������������������ȥ����An������Ϊ__��
x����A1����Ϊ��1��0��������A1��x��Ĵ��߽�ֱ���ڵ�B1����ԭ��OΪԲ�ģ�OB1��Ϊ�뾶������x���ڵ�A2���ٹ���A2��x��Ĵ��߽�ֱ���ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������x���ڵ�A3��������������������ȥ����An������Ϊ__��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=��![]() x+3��x�ᡢy��ֱ��ཻ�ڵ�A��B���ٽ���A0B��ֱǮCD�۵���ʹ��A���B�غϣ��ۺ�CD��x�ύ�ڵ�C����AB���ڵ�D��
x+3��x�ᡢy��ֱ��ཻ�ڵ�A��B���ٽ���A0B��ֱǮCD�۵���ʹ��A���B�غϣ��ۺ�CD��x�ύ�ڵ�C����AB���ڵ�D��
��1����A��������������B������������
��2����OC�ij��ȣ��������ʱֱ��BC�ı���ʽ��
��3��ֱ��BC���Ƿ����һ��M��ʹ�á�ABM��������ABO�������ȣ������ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AC=4 ![]() ��BD=4������P���߶�BD�ϴӵ�B���D�˶���PF��AB�ڵ�F���ı���PFBG����BD�Գƣ��ı���QEDH���ı���PFBG����AC�Գƣ�������ABCD���������ı��θ�ס���ֵ����ΪS1 �� δ����ס���ֵ����ΪS2 �� BP=x��
��BD=4������P���߶�BD�ϴӵ�B���D�˶���PF��AB�ڵ�F���ı���PFBG����BD�Գƣ��ı���QEDH���ı���PFBG����AC�Գƣ�������ABCD���������ı��θ�ס���ֵ����ΪS1 �� δ����ס���ֵ����ΪS2 �� BP=x�� 
��1���ú�x�Ĵ���ʽ�ֱ��ʾS1 �� S2��
��2����S1=S2 �� ��x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Բ����������������Ⱥ��Բ��ƣ��ĸ�Ϊ12cm�������ܳ�Ϊ10cm���������ڱ��������ײ�3cm�ĵ�B����һ��������ʱһֻ����������������ڣ�������������3cm�ĵ�A���������ϳԵ����������е����·���Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1��x���ڵ�A��2��0������B��ֱ��l1�ϵĶ��㣮ֱ��l2��y=x+1��l1�ڵ�C������B��ֱ��l3��ֱ��l2 �� ����ΪD������O��B��ֱ��l4��l2�ڵ�E����ֱ��l1 �� l2 �� l3��Χ��������ʱ��������������ΪS1 �� ��ֱ��l2 �� l3 �� l4��Χ��������ʱ��������������ΪS2 �� 
��1������B���߶�AC�ϣ���S1=S2 �� ��B������Ϊ��
��2������B��ֱ��l1�ϣ���S2= ![]() S1 �� ���BOA�Ķ���Ϊ ��
S1 �� ���BOA�Ķ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=a��x��1��2+4��x�ύ�ڵ�A��B����y�ύ�ڵ�C������C��CD��x�ύ�����ߵĶԳ����ڵ�D������BD����֪��A������Ϊ����1��0�� 
��1����������ߵĽ���ʽ��
��2��������COBD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�У�AB=4��AD=3��P��Q�ǶԽ���BD�ϲ��غϵ����㣬��P����ֱ��AD��AB�ĶԳƵ�ֱ��ǵ�E��F����Q����ֱ��BC��CD�ĶԳƵ�ֱ��ǵ�G��H�����ɵ�E��F��G��H���ɵ��ı���ǡ��Ϊ���Σ���PQ�ij�Ϊ ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com