
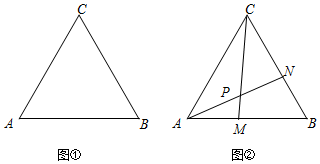
���� ��1�����������������ͼ1������BNM=90��ʱ����BMN=30�㣬��BM=2BN������ͼ2������BMN=90��ʱ����BNM=30�㣬BN=2BM���ֱ���ʽ�����t��ֵ��
��2����ͼ3����BM=BNʱ����ABN�ա�CBM����AM=BM������t=6-t��������ɣ�
��3����ͼ4����CPN�Ķ������ᷢ���仯��������60�㣬֤����CAM�ա�ABN����������Ƕ������Եó����ۣ�
���  �⣺��1��������ã�AM=BN=t����BM=6-t
�⣺��1��������ã�AM=BN=t����BM=6-t
����BMN��ֱ��������ʱ�������������
����ͼ1������BNM=90��ʱ��
�ߡ�ABC�ǵȱ������Σ�
���B=60�㣬
���BMN=90��-60��=30�㣬
��BM=2BN��
��6-t=2t��
t=2��
����ͼ2������BMN=90��ʱ��
�ߡ�B=60�㣬
���BNM=30�㣬
��BN=2BM��
��t=2��6-t����
t=4��
������������t=2��4ʱ����BMN��ֱ�������Σ�
�ʴ�Ϊ��2��4��
��2����ͼ3����AB=BC����B=��B��
�൱BM=BNʱ����ABN�ա�CBM��
��AM=BN��
��AM=BM��
��t=6-t��
t=3��
�൱t=3ʱ����ABN�ա�CBM��
�ʴ�Ϊ��3��
��3����M��N���˶��Ĺ����У���CPN�Ķ������ᷢ���仯��������60�㣬�����ǣ�
��ͼ4��
�ڡ�CAM�͡�ABN�У�
��$\left\{\begin{array}{l}{AC=AB}\\{��CAB=��ABC=60��}\\{AM=BN}\end{array}\right.$��
���CAM�ա�ABN��SAS����
���ACM=��BAN��
�ߡ�BAN+��CAN=��CAB=60�㣬
���ACM+��CAN=60�㣬
�ߡ�CPN=��ACM+��CAN��
���CPN=60�㣮
���� ���⿼���˵ȱ������Ρ�ȫ�������ε����ʺ��ж��Լ������˶����⣬�Ѷ����У����п��������ͣ��ڶ��������У���ͼ�ٶ���ȣ�ʱ����ȣ���·����ȣ�ͬʱ�ڵ�1���в����˷������۵�˼�룬�����⣬Ҫע�⣮


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
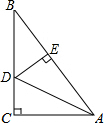 ��ͼ����ABC�У���C=90�㣬��B=30�㣬ADƽ�֡�BAC��CD=2cm��DE��AB��E����BD=��������
��ͼ����ABC�У���C=90�㣬��B=30�㣬ADƽ�֡�BAC��CD=2cm��DE��AB��E����BD=��������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 2 | C�� | -2 | D�� | -3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com