
【题目】如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD.
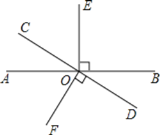
(1)图中与∠AOF互余的角是 _________ ;与∠COE互补的角是 _______ __ .(把符合条件的角都写出来)
(2)如果∠AOC=![]() ∠EOF,求∠AOC的度数.
∠EOF,求∠AOC的度数.
【答案】(1)∠AOC、∠BOD;∠EOD、∠BOF;(2)36°.
【解析】
(1)根据互为余角的和等于90°,结合图形找出即可,再根据对顶角相等找出相等的角;根据互为补角的和等于180°,结合图形找出,然后根据对顶角相等找出相等的角;
(2)设∠AOC=x,则∠EOF=4x,根据对顶角相等可得∠BOD=x,然后利用周角等于360°列式进行计算即可求解.
(1)图中与∠AOF互余的角是∠AOC、∠BOD;
图中与∠COE互补的角是∠EOD、∠BOF;
(2)∵OE⊥AB,OF⊥CD,
∴∠EOB=90°∠FOD=90°,
∵∠AOC=![]() ∠EOF,
∠EOF,
∴设∠AOC=x,则∠BOD=x,∠EOF=4x,
4x+x+90°+90°=360°,
解得x=36°,
∴∠AOC=36°.


科目:初中数学 来源: 题型:
【题目】乘法公式的探究与应用:

(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分面积是 (写成两数平方差的形式)
(2)小颖将阴影部分裁下来,重新拼成一个长方形,如图乙,则长方形的长是 ,宽是 ,面积是 (写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到公式 (用式子表达)
(4)运用你所得到的公式计算:10.3×9.7.
查看答案和解析>>
科目:初中数学 来源: 题型:
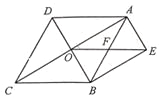
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=10,AC=16,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在创建文明城区的活动中,有两端长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度![]() (米)与施工时间
(米)与施工时间![]() (时)之间的关系的部分图像.请解答下列问题.
(时)之间的关系的部分图像.请解答下列问题.
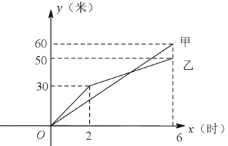
(1)甲队在![]() 的时段内的速度是 米/时.乙队在
的时段内的速度是 米/时.乙队在![]() 的时段内的速度是 米/时. 6小时甲队铺设彩色道砖的长度是 米,乙队铺设彩色道砖的长度是 米.
的时段内的速度是 米/时. 6小时甲队铺设彩色道砖的长度是 米,乙队铺设彩色道砖的长度是 米.
(2)如果铺设的彩色道砖的总长度为150米,开挖6小时后,甲队、乙队均增加人手,提高了工作效率,此后乙队平均每小时比甲队多铺5米,结果乙反而比甲队提前1小时完成总铺设任务.求提高工作效率后甲队、乙队每小时铺设的长度分别为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
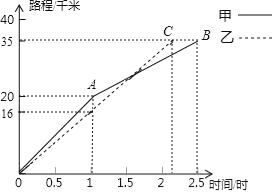
【题目】2018年,广州国际龙舟邀请赛于6月23日在中山大学北门广场至广州大桥之间的珠江河段举行.上午8时,参赛龙舟同时出发,甲、乙两队在比赛中,路程y(千米)与时间x(小时)的函数关系如图所示,甲队在上午11时30分到达终点.
(1)在比赛过程中,乙队何时追上甲队?
(2)在比赛过程中,甲、乙两队何时相距最远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=120°,△ABC是等边三角形,O点是边BC的中点,将△ABC绕点O逆时针旋转一定的角度,OM与边AB相交于点D,ON与边AC(或AC的延长线)相交于点E.
(1)如图1,若OD⊥AB,垂足为D,BC=4,求CE的长;
(2)如图2,当ON与AC边交于点E时,求证:BD+CE=![]() BC;
BC;
(3)如图3,当ON与AC边的延长线交于点E时,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BD、BC、CE之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点,一次函数y=![]() x+1的图象为直线l2,与x轴交于点C,两直线l1,l2相交于点B.
x+1的图象为直线l2,与x轴交于点C,两直线l1,l2相交于点B.
(1)求k,b的值;
(2)求点B的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CE平分∠ACB,CE⊥AB于点 E,过 E作 ED∥AC交 BC于点 D,过 D作 DF⊥AB于点 F.
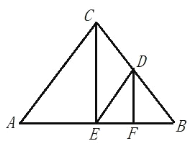
(1)若∠ACE=40°,求∠EDC的度数.
(2)判断∠EDF与∠BDF是否相等,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0).
(1)求抛物线的表达式,并写出其顶点坐标;
(2)现将此抛物线沿y轴方向平移若干个单位,所得抛物线的顶点为D,与y轴的交点为B,与x轴负半轴交于点A,过B作x轴的平行线交所得抛物线于点C,若AC∥BD,试求平移后所得抛物线的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com