练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．某种出租车的收费标准是：起步价6元（即行驶距离不超过3千米都需付6元车费），超过3千米，每增加1千米，加收1.5元（不足1千米按1千米计）．某人乘这种出租车从甲地到乙地共支付车费21元，设此人从甲地到乙地经过的路程是x千米，那么x的最大值是（　　）
    A．10B．15C．13D．14

    分析 已知从甲地到乙地共需支付车费21元，从甲地到乙地经过的路程为x千米，从而根据题意列出不等式，从而得出答案．

    解答 解：设此人从甲地到乙地经过的路程是x千米，根据题意，
    得：6+1.5（x-3）≤21，
    解得：x≤13，
    ∴此人从甲地到乙地经过的路程是x的最大值为13km，
    故选：C．

    点评 本题考查了一元一次不等式的应用，将现实生活中的事件与数学思想联系起来，读懂题列出不等式关系式即可求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．分解因式：
    （1）6a2b-4a3b3-2ab               
    （2）25m2-n2
    （3）4x2+12xy+9y2
    （4）a2（x-y）-b2（x-y）
    （5）-2a2x4+16a2x2-32a2
    （6）（a2-a）2-（a-1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．某学校实验学案教学，需印制若干份学案，印刷厂有甲、乙两种收费方式：甲种方式要收取制版费6元，每份学案收印刷费0.1元；乙种方式不收取制版费，每份收取印刷费0.12元．
    （1）直接写出两种收费方式的费用y甲（元）、y乙（元）与印刷份数x（份）之间的函数关系式；
    （2）若该学校某年级每次需印制x（280≤x≤320）份学案，通过计算说明学校选择哪种收费方式比较合算．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．则下列结论：①A，B两城相距300千米；②乙车比甲车晚出发1小时，却早到1小时；③乙车出发后2.5小时追上甲车：④当甲、乙两车相距50千米时，$t=\frac{5}{4}$或$\frac{15}{4}$．其中不正确的结论是③④（填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

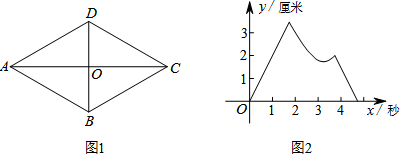
    19．如图1，四边形ABCD是菱形，对角线AC，BD相交于点O，AB=2厘米，∠BAD=60°．P，Q两点同时从点O出发，以1厘米/秒的速度在菱形的对角线及边上运动．设运动的时间为x秒，P，Q间的距离为y厘米，y与x的函数关系的图象大致如图2所示，则P，Q的运动路线可能为（　　）
    A．点P：O-A-D-C，点Q：O-C-D-OB．点P：O-A-D-O，点Q：O-C-B-O
    C．点P：O-A-B-C，点Q：O-C-D-OD．点P：O-A-D-O，点Q：O-C-D-O

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列方程中，无实数解的是（　　）
    A．2+x=0B．2-x=0C．2x=0D．$\frac{2}{x}$=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．先化简，再求值：a（a-2）-（a+3）（a-3），其中a=-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图1和2，四边形ABCD是菱形，点P是对角线AC上一点，以点P为圆心，PB为半径的弧，交BC的延长线于点F，连接PF，PD，PB．
    （1）如图1，点P是AC的中点，请写出PF和PD的数量关系：PF=PD；
    （2）如图2，点P不是AC的中点，
    ①求证：PF=PD．
    ②若∠ABC=50°，直接写出∠DPF的度数．

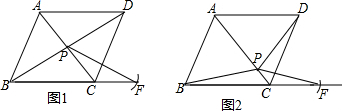
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

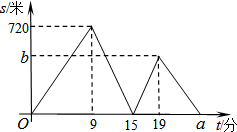    14．小强、小林从学校出发，沿着笔直的道路去少年宫参加书法比赛，小强步行去少年宫一段时间后，小林骑自行车去少年宫，两人均匀速前行．他们两人之间的距离s（米）与小强出发时间t（分）之间的函数关系如图．
    结合图象信息，小成给出如下说法：
    ①小林先到达少年宫；②小林的速度是小强速度的2.5倍；③小强出发24分钟时到达少年宫；④小强出发19分钟时，小林还需要继续行进480米才能到达少年宫．
    其中正确的说法是（　　）
    A．①②B．②④C．①③④D．①②④

    查看答案和解析>>

    同步练习册答案