
分析 利用反证法,结合任何有理数都可以表示成$\frac{q}{p}$的形式(p,q都是整数),反过来也一样,任何形如$\frac{q}{p}$(p,q都是整数)的数都是有理数,即可证明结论.
解答 证明:(1)任何有理数都可以表示成$\frac{q}{p}$的形式(p,q都是整数),反过来也一样,任何形如$\frac{q}{p}$(p,q都是整数)的数都是有理数,
∵a为有理数,
∴a=$\frac{q}{p}$.
如果a+x是有理数,那么a+x=$\frac{q′}{p′}$,x=$\frac{q′}{p′}$-a=$\frac{q′}{p′}$-$\frac{q}{p}$=$\frac{pq′-qp′}{pp′}$,
那么x是有理数,这与x为无理数矛盾,
所以a+x为无理数;
(2)如果ax是有理数,那么ax=$\frac{q′}{p′}$,x=$\frac{pq′}{qp′}$
所以x是有理数,这与x为无理数矛盾,
所以当a≠0时,ax为无理数.
点评 本题考查了反证法,考查学生分析解决问题的能力,正确运用反证法是关键.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:填空题
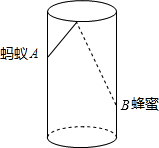 如图,圆柱形容器杯高16cm,底面周长20cm,在离杯底3cm的点B处有一滴蜂蜜,此时蚂蚁在离杯上沿2cm与蜂蜜相对的A处,则蚂蚁从A处爬到B处的蜂蜜最短距离为5$\sqrt{13}$.
如图,圆柱形容器杯高16cm,底面周长20cm,在离杯底3cm的点B处有一滴蜂蜜,此时蚂蚁在离杯上沿2cm与蜂蜜相对的A处,则蚂蚁从A处爬到B处的蜂蜜最短距离为5$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com