
分析 (1)一元二次方程x2-2x+m=0有两个实数根,△≥0,把系数代入可求m的范围;
(2)利用两根关系,已知x1+x2=2结合x1+3x2=3,先求x1、x2,再求m.
解答 解:(1)∵方程x2-2x+m=0有两个实数根,
∴△=(-2)2-4m≥0,
解得m≤1;
(2)由两根关系可知,x1+x2=2,x1•x2=m,
解方程组$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=2}\\{{x}_{1}+3{x}_{2}=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=\frac{3}{2}}\\{{x}_{2}=\frac{1}{2}}\end{array}\right.$,
∴m=x1•x2=$\frac{3}{4}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的根与系数的关系.


科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,AB≠CD,E、F、G、H分别是AB、BD、CD、AC的中点.
如图,四边形ABCD中,AB≠CD,E、F、G、H分别是AB、BD、CD、AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 抽取的乒乓球数n | 50 | 100 | 200 | 500 | 1000 | 1500 | 2000 |
| 优等品的频数m | 48 | 95 | 188 | 471 | 946 | 1426 | 1898 |
| 优等品的频率$\frac{m}{n}$ | 0.960 | 0.950 | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
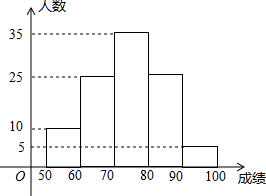 某校八年级同学进行物理知识竞赛,从中随机抽取100人的成绩进行整理,每个小组的分组标准是:50≤x<60,60≤x<70…,画出频数分布直方图如下:
某校八年级同学进行物理知识竞赛,从中随机抽取100人的成绩进行整理,每个小组的分组标准是:50≤x<60,60≤x<70…,画出频数分布直方图如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,直线EF绕对角线AC的中点O旋转,分别交BC、AD于E、F两点,连接AE、CF.
如图,在平行四边形ABCD中,直线EF绕对角线AC的中点O旋转,分别交BC、AD于E、F两点,连接AE、CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
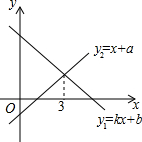 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①当x<3时,y1>0;②当x<3时,y2>0;③当x>3时,y1<y2中,正确的个数是( )
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①当x<3时,y1>0;②当x<3时,y2>0;③当x>3时,y1<y2中,正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
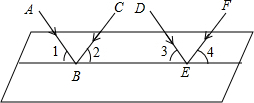 如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4.
如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com