
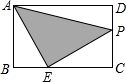
 如图,在矩形ABCD中,AB=2,AD=3,BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是
如图,在矩形ABCD中,AB=2,AD=3,BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是| A. |  | B. | 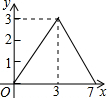 | C. | 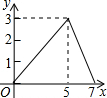 | D. |  |
分析 求出CE的长,然后分①点P在AD上时,利用三角形的面积公式列式得到y与x的函数关系;②点P在CD上时,根据S△APE=S梯形AECD-S△ADP-S△CEP列式整理得到y与x的关系式;③点P在CE上时,利用三角形的面积公式列式得到y与x的关系式,然后选择答案即可.
解答 解:∵在矩形ABCD中,AB=2,AD=3,
∴CD=AB=2,BC=AD=3,
∵BE=1,
∴CE=BC-BE=2,
①点P在AD上时,△APE的面积y=$\frac{1}{2}$x•2=x(0≤x≤3),
②点P在CD上时,S△APE=S梯形AECD-S△ADP-S△CEP,
=$\frac{1}{2}$(2+3)×2-$\frac{1}{2}$×3×(x-3)-$\frac{1}{2}$×2×(3+2-x),
=5-$\frac{3}{2}$x+$\frac{9}{2}$-5+x,
=-$\frac{1}{2}$x+$\frac{9}{2}$,
∴y=-$\frac{1}{2}$x+$\frac{9}{2}$(3<x≤5),
③点P在CE上时,S△APE=$\frac{1}{2}$×(3+2+2-x)×2=-x+7,
∴y=-x+7(5<x≤7),
故选:A.
点评 本题考查了动点问题函数图象,读懂题目信息,根据点P的位置的不同分三段列式求出y与x的关系式是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -3 | C. | -4 | D. | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com