如图，点B1在反比例函数y=
（x＞0）的图象上，过点B1分别作x轴和y轴的垂线，垂足为C1和A，得到第一个矩形AOC1B1，点C1的坐标为（1，0）；取x轴上一点C2（
，0），过点C2作x轴的垂线交反比例函数图象于点B2，过B2作线段B2 A1⊥B1C1，，交B1C1于点A1，得到第二个矩形A1C1C2B2；依次在x轴上取点C3（2，0），
C4（
，0）…按此规律作矩形，则第10个矩形A9C9C10B10的面积为 ．
科目：初中数学 来源： 题型：
阅读下列材料：
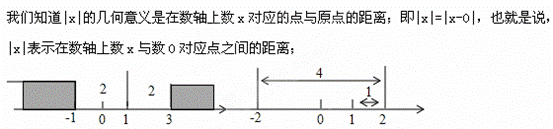
这个结论可以推广为|x1-x2|表示在数轴上数x1，x2对应点之间的距离；
在解题中，我们会常常运用绝对值的几何意义：
例1：解方程|x|=2．容易得出，在数轴上与原点距离为2的点对应的数为±2，即该方程的x=±2；
例2：解不等式|x-1|＞2．如图，在数轴上找出|x-1|=2的解，即到1的距离为2的点对应的数为-1，3，则|x-1|＞2的解为x＜-1或x＞3；
例3：解方程|x-1|+|x+2|=5．由绝对值的几何意义知，该方程表示求在数轴上与1和-2的距离之和为5的点对应的x的值．在数轴上，1和-2的距离为3，满足方程的x对应点在1的右边或-2的左边．若x对应点在1的右边，如图可以看出x=2；同理，若x对应点在-2的左边，可得x=-3．故原方程的解是x=2或x=-3．
参考阅读材料，解答下列问题：
（1）方程|x+3|=4的解为 .
1或-7
（2）解不等式|x-3|+|x+4|≥9.
（3）若|x-3|-|x+4|≤a对任意的x都成立，求a的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，这三种可能性大小相同，现在两辆汽车经过这个十字路口．
（1）请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果；
（2）求这两辆汽车都向左转的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
根据图中所给的数据，求得避雷针CD的长约为__m（结果精确到0.01 m）．（可用计算器求，也可用下列参考数据求：sin ≈0.682 0，sin 40°≈0.642 8，cos 43°≈0.731 4，cos 40°≈0.766 0，tan 43°≈0.932 5，tan 40°≈0.839 1）
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，梯形ABCD中，AD∥BC，∠B＝45°，∠D＝120°，AB＝6
cm，则DC的长为 ( )
A．2 
cm B．
2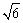 
cm C．4 cm D．4 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
2倍 C.不变
D.不能确定