


科目:初中数学 来源: 题型:
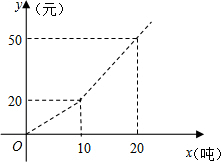 采取分段收费标准,右图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.
采取分段收费标准,右图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 我国是水资源严重缺乏的国家,今年上半年长江中下游地区发生严重旱灾,为鼓励节约用水,某市自来水公司采取分段收费标准,右图反映的毎月收取水费y(元)与用水量x(吨)之间的函数关系.
我国是水资源严重缺乏的国家,今年上半年长江中下游地区发生严重旱灾,为鼓励节约用水,某市自来水公司采取分段收费标准,右图反映的毎月收取水费y(元)与用水量x(吨)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com