
 (2013•池州一模)如图是一个外轮廓为矩形的机器零件平面示意图,根据图中标出尺寸(单位:mm)计算两圆孔中心A和B的距离为
(2013•池州一模)如图是一个外轮廓为矩形的机器零件平面示意图,根据图中标出尺寸(单位:mm)计算两圆孔中心A和B的距离为 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
 (2013•池州一模)如图是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出(球可以经过多次反射),则该球最后将落入的球袋是( )
(2013•池州一模)如图是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出(球可以经过多次反射),则该球最后将落入的球袋是( )查看答案和解析>>
科目:初中数学 来源: 题型:
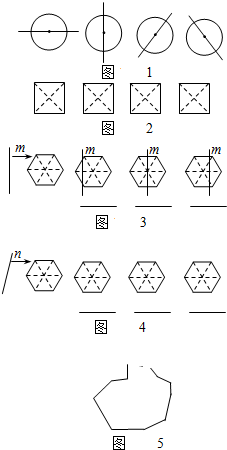 (2013•池州一模)我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1).
(2013•池州一模)我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com