
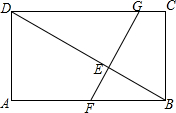
 如图,在矩形ABCD中,AB=9,AD=3$\sqrt{3}$,E为对角线BD上一点,且DE=2BE,过E作FG⊥BD,分别交AB、CD于F、G.将四边形BCGF绕点B旋转180°,在此过程中,设直线GF分别与直线CD、BD交于点M、N,当△DMN是以∠MDN为底角的等腰三角形时,则DN的长是10$\sqrt{3}$或6$\sqrt{3}$-4.
如图,在矩形ABCD中,AB=9,AD=3$\sqrt{3}$,E为对角线BD上一点,且DE=2BE,过E作FG⊥BD,分别交AB、CD于F、G.将四边形BCGF绕点B旋转180°,在此过程中,设直线GF分别与直线CD、BD交于点M、N,当△DMN是以∠MDN为底角的等腰三角形时,则DN的长是10$\sqrt{3}$或6$\sqrt{3}$-4. 分析 先根据解直角三角形,求得BF的长,再根据旋转求得BF'的长,最后根据四边形BCGF旋转后的两种不同位置进行讨论,求得DN的长.
解答 解:∵矩形ABCD中,AB=9,AD=3$\sqrt{3}$,
∴∠DBA=∠MDN=30°,BD=6$\sqrt{3}$
∵DE=2BE,
∴BE=2$\sqrt{3}$,
∵FG⊥BD,
∴BF=$\frac{BE}{cos∠EBF}$=$\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=4
由旋转可得BF'=BF=4,∠F'BC'=∠FBC=90°,∠BFG=∠BF'G'=60°
①如图,当△DMN是以∠MDN、∠MND为底角的等腰三角形时,∠N=30°
∴tan∠BNF'=$\frac{BF'}{BN}$=$\frac{\sqrt{3}}{3}$
∴$\frac{4}{BN}=\frac{\sqrt{3}}{3}$,即BN=4$\sqrt{3}$
∴DN=BD+BN=6$\sqrt{3}$+4$\sqrt{3}$=10$\sqrt{3}$;
②如图,当△DMN是以∠MDN、∠NMD为底角的等腰三角形时,∠BNM=60°=∠BF'M,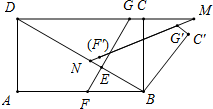
此时,F'与N重合,故BF'=BN=4
∴DN=BD-BN=6$\sqrt{3}$-4.
故答案为:10$\sqrt{3}$或6$\sqrt{3}$-4
点评 本题主要考查了旋转的性质,解决问题的关键是根据旋转的不同角度,得到△DMN是以∠MDN、∠MND为底角的等腰三角形或以∠MDN、∠NMD为底角的等腰三角形.解题时注意,等腰三角形的问题一般需要考虑进行分类讨论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
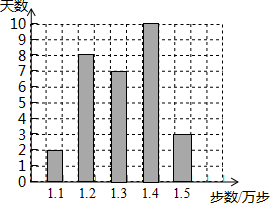 赵老师是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( )
赵老师是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( )| A. | 1.2,1.3 | B. | 1.4,1.3 | C. | 1.4,1.35 | D. | 1.3,1.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com