
 ��ͼ������ֽƬABCD�ı߳�Ϊ2���۵�����ֽƬ����B��D�����غ��ڶԽ���BD�ϵ�ͬһ��P�����ۺ۷ֱ�ΪEF��GH���غϵ�P�ڶԽ���BD���ƶ������ۺ�EF�ij�Ϊm������ֱ��ж����½��۵���٣����������ɣ�
��ͼ������ֽƬABCD�ı߳�Ϊ2���۵�����ֽƬ����B��D�����غ��ڶԽ���BD�ϵ�ͬһ��P�����ۺ۷ֱ�ΪEF��GH���غϵ�P�ڶԽ���BD���ƶ������ۺ�EF�ij�Ϊm������ֱ��ж����½��۵���٣����������ɣ����� ��1�����������֪��BEF�͡�DGH�ǵȱ������Σ��ٸ������ε����ʼ�����⣻
��2�����������֪�ı���BEPF���ı���DGPH�������Σ��ٸ��������ε����ʼ�����⣻
��3�����������֪EF+GH=AC���ٸ������Ǻ�����������ʼ�����⣻
��4�����������֪EF+GH=AC���ٸ������Ǻ��������ε����ʼ�����⣮
��� �⣺��1����������ABC=60�㣬�������֪��BEF�͡�DGH�ǵȱ������Σ�
��EF+AE+AG+GH+CH+CF=BE+AE+AG+GD+DH+CH=2+2+2=6��
��������AEFCHG���ܳ�Ϊ 6��������AEFCHG���ܳ�Ϊ6�Ƕ�ֵ�����ۺ�EF�ij�m�أ�
��2���ԣ�����ABC=90�㣬${S_{AEFCHG}}={S_{��BCD}}+{S_{AEPG}}=2+\frac{{\sqrt{2}m}}{2}��2-\frac{{\sqrt{2}m}}{2}��=-\frac{1}{2}{m^2}+\sqrt{2}m+2$SAEFCHG���ֵ=$\frac{{4����-\frac{1}{2}����2-{{��\sqrt{2}��}^2}}}{{4����-\frac{1}{2}��}}=3$��
��3���ԣ�SAEFCHG=S��BCD+SAEPG=$\frac{{\sqrt{3}}}{4}��{2^2}$+$\frac{{\sqrt{3}m}}{3}��2-\frac{{\sqrt{3}m}}{3}����\frac{{\sqrt{3}}}{2}$=$-\frac{{\sqrt{3}}}{6}{m^2}+m+\sqrt{3}$��0��m��2$\sqrt{3}$����
��4���ԣ�����ABC�Ĵ�СΪ2�����������֪EF+GH=AC����������AEFCHG���ܳ��ɱ�ʾΪ2��2+2��sin����2=4+4sin����
���� �����˷��۱任���۵����⣩�����ε����ʣ�����ؼ��ǵõ�EF+GH=AC���ۺ��Խ�ǿ����һ�����Ѷ�


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ֱ��AB��CD�ཻ�ڵ�O����AOD=100�㣬���AOC�Ķ���Ϊ��������
��ͼ��ֱ��AB��CD�ཻ�ڵ�O����AOD=100�㣬���AOC�Ķ���Ϊ��������| A�� | 120�� | B�� | 100�� | C�� | 90�� | D�� | 80�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼΪ�ס��ҡ���������ֱ��ľ��ƽ�аڷ��ڵ����ϵ����Σ���֪����һ����ֻ����ص������ಿ��ֻ����ص�����û�������ص��IJ��ֵij���Ϊ1���ߣ���û�������ص��IJ��ֵij���Ϊ2���ߣ����ҵij�����Ҽס��ҵij������x���ߣ��ҡ����ij������y���ߣ����ҵij���Ϊ���ٹ��ߣ���������
��ͼΪ�ס��ҡ���������ֱ��ľ��ƽ�аڷ��ڵ����ϵ����Σ���֪����һ����ֻ����ص������ಿ��ֻ����ص�����û�������ص��IJ��ֵij���Ϊ1���ߣ���û�������ص��IJ��ֵij���Ϊ2���ߣ����ҵij�����Ҽס��ҵij������x���ߣ��ҡ����ij������y���ߣ����ҵij���Ϊ���ٹ��ߣ���������| A�� | x+y+3 | B�� | x+y+1 | C�� | x+y-1 | D�� | x+y-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
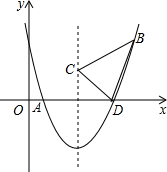 ��ͼ�����κ���y=$\frac{1}{2}$x2+bx+c��ͼ��x����A��D���㣬������B�㣬��֪A�������ǣ�2��0����B�������ǣ�8��6����
��ͼ�����κ���y=$\frac{1}{2}$x2+bx+c��ͼ��x����A��D���㣬������B�㣬��֪A�������ǣ�2��0����B�������ǣ�8��6�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | С���ľ�������������� | |
| B�� | С���ľ����������� | |
| C�� | ������������ٵ������У�С���ľ�����������ڵ�ʮ��λ | |
| D�� | ������������ٵ������У�С���ľ����һ���ȵ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������OABC����������A��C�ֱ���y���x���ϣ���AB��BC�뷴��������y1=$\frac{4}{x}$��x��0����y2=$\frac{k}{x}$��k��0��x��0��ͼ����E��F�͵�H��G��AE��AF=2��3��
��ͼ������OABC����������A��C�ֱ���y���x���ϣ���AB��BC�뷴��������y1=$\frac{4}{x}$��x��0����y2=$\frac{k}{x}$��k��0��x��0��ͼ����E��F�͵�H��G��AE��AF=2��3���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com