
分析 (1)根据有理数的乘方的定义分别进行计算,再进行比较即可;
(2)根据上述得出的答案解答即可;
(3)①根据(2)的结论解答即可,②根据不等式性质,两边同时除以-1,不等号方向不变;
(4)分别通分后,比较分子的大小即可.
解答 解:(1)①12=1,21=2,则12<21;
②23=8,32=9,则23<32;
③34=81,43=64,则34>43;
④45=1024,54=625,则45>54;
⑤56=15625,65=7776,则56>65;
故答案为:<,<,>,>,>;
(2)从上面的结果经过归纳,可以猜想出nn+1和(n+1)n的大小关系是:
当n<3时,nn+1<(n+1)n,
当n≥3时,nn+1>(n+1)n;
故答案为:>;
(3)①∵2010>3,
∴20102011>20112010.
②-20102011<-20112010,
故答案为:>,<;
(4)∵$\frac{{2}^{2011}+1}{{2}^{2012}+1}$=$\frac{({2}^{2011}+1)({2}^{2013}+1)}{({2}^{2012}+1)({2}^{2013}+1)}$=$\frac{{2}^{4024}+{2}^{2011}+{2}^{2013}+1}{({2}^{2012}+1)({2}^{2013}+1)}$,
$\frac{{2}^{2012}+1}{{2}^{2013}+1}$=$\frac{({2}^{2012}+1)^{2}}{({2}^{2012}+1)({2}^{2013}+1)}$,
∵(22012+1)2=24024+2×22012+1=24024+22013+1<24024+22011+22013+1,
∴$\frac{{2}^{2011}+1}{{2}^{2012}+1}$>$\frac{{2}^{2012}+1}{{2}^{2013}+1}$;
故答案为:>.
点评 本题考查了有理数的乘方,有理数的大小比较、不等式的性质,理解有理数的乘方的意义准确计算是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
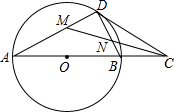 如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.
如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
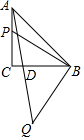 如图,△ABC是等腰直角三角形,∠C=90°,点P是直线AC上一个动点,连结BP,过点B作BQ⊥BP,且使BP=BQ,连结AQ且与直线BC相交于点D.若AP=2,AC=5,则BD的长为4或6.
如图,△ABC是等腰直角三角形,∠C=90°,点P是直线AC上一个动点,连结BP,过点B作BQ⊥BP,且使BP=BQ,连结AQ且与直线BC相交于点D.若AP=2,AC=5,则BD的长为4或6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≤-l | B. | a≤-2 | C. | a≤1且a≠-2 | D. | a≤-1且a≠-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com