
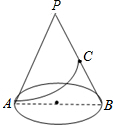
 己知底面半径是4cm,母线长为12cm,C为母线PB中点,现在有一只蚂蚁从底边一点A出发.在侧面爬行到C点,则蚂蚁在圆锥侧面爬行最短距离6$\sqrt{3}$cm.
己知底面半径是4cm,母线长为12cm,C为母线PB中点,现在有一只蚂蚁从底边一点A出发.在侧面爬行到C点,则蚂蚁在圆锥侧面爬行最短距离6$\sqrt{3}$cm. 分析 最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.需先算出圆锥侧面展开图的扇形半径.看如何构成一个直角三角形,然后根据勾股定理进行计算.
解答  解:圆锥的底面周长是2π×2=8π,则8π=$\frac{nπ×12}{180}$,
解:圆锥的底面周长是2π×2=8π,则8π=$\frac{nπ×12}{180}$,
∴n=120°,
即圆锥侧面展开图的圆心角是120度.
∴∠APB=60°,
∵PA=PB,
∴△PAB是等边三角形,
∵C是PB中点,
∴AC⊥PB,
∴∠ACP=90度.
∵在圆锥侧面展开图中AP=12,PC=6,
∴在圆锥侧面展开图中AC=$\sqrt{A{P}^{2}-P{C}^{2}}$=6$\sqrt{3}$(cm).
最短距离是6$\sqrt{3}$cm.
故答案为:6$\sqrt{3}$cm.
点评 本题考查了圆锥的计算,需注意最短距离的问题最后都要转化为平面上两点间的距离的问题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com