
【题目】机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.
(1)求弦BC的长;
(2)求圆O的半径长.
(本题参考数据:sin 67.4° =![]() ,cos 67.4°=
,cos 67.4°=![]() ,tan 67.4° =
,tan 67.4° =![]() )
)

科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程x2-(k+2)x+k-1=0
的一元二次方程x2-(k+2)x+k-1=0
(1)若方程的一个根为 -1,求![]() 的值和方程的另一个根;
的值和方程的另一个根;
(2)求证:不论![]() 取何值,该方程都有两个不相等的实数根.
取何值,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,且
,且![]() 于
于![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 边的中点,连接
边的中点,连接![]() 与
与![]() 相交于点
相交于点![]() ,下列结论正确的有( )个
,下列结论正确的有( )个
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是等腰三角形;⑤
是等腰三角形;⑤![]() .
.

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程
解:设x2﹣4x=y,
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
(1)该同学第二步到第三步运用了因式分解的 (填序号).
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学在第四步将y用所设中的x的代数式代换,得到因式分解的最后结果.这个结果是否分解到最后? .(填“是”或“否”)如果否,直接写出最后的结果 .
(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的 日销售量(件)与时间(天)的关系如下表:
时间(天) | 1 | 3 | 6 | 10 | 36 | … |
日销售量(件) | 94 | 90 | 84 | 76 | 24 | … |
未来40天内,前20天每天的价格y1(元/件)与t时间(天)的函数关系式为:y1=![]() t+25(1≤t≤20且t为整数);后20天每天的价格y2(原/件)与t时间(天)的函数关系式为:y2=—
t+25(1≤t≤20且t为整数);后20天每天的价格y2(原/件)与t时间(天)的函数关系式为:y2=—![]() t+40(21≤t≤40且t为整数).下面我们来研究 这种商品的有关问题.
t+40(21≤t≤40且t为整数).下面我们来研究 这种商品的有关问题.
(1)认真分析上表中的数量关系,利用学过的一次函数、二次函数 、反比例函数的知识确定一个满足这些数据之间的函数关系式;
(2)请预测未来40天中那一天的销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程,公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以每小时60千米/时的速度沿此公路从
两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以每小时60千米/时的速度沿此公路从![]() 地匀速开往
地匀速开往![]() 地,乙车从
地,乙车从![]() 地沿此公路匀速开往
地沿此公路匀速开往![]() 地,两车分别到达目的地后停止甲、乙两车相距的路程
地,两车分别到达目的地后停止甲、乙两车相距的路程![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (时)之间的函数关系如图所示:
(时)之间的函数关系如图所示:
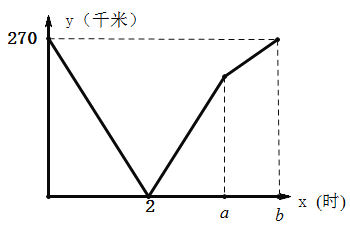
(1)乙年的速度为______千米/时,![]() _____,
_____,![]() ______.
______.
(2)求甲、乙两车相遇后![]() 与
与![]() 之间的函数关系式,并写出相应的自变量
之间的函数关系式,并写出相应的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l1:y=﹣2x+6与坐标轴交于A,B两点,直线l2:y=kx+2(k>0)与坐标轴交于点C,D,直线l1,l2与相交于点E.
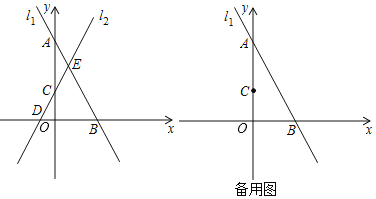
(1)当k=2时,求两条直线与x轴围成的△BDE的面积;
(2)点P(a,b)在直线l2:y=kx+2(k>0)上,且点P在第二象限.当四边形OBEC的面积为![]() 时.
时.
①求k的值;
②若m=a+b,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )
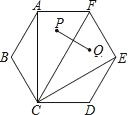
A. 1 B. 2 C. 2![]() ﹣2 D. 4﹣2
﹣2 D. 4﹣2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com