
【题目】对于二次函数 ![]() 的图象与性质,下列说法正确的是( )
的图象与性质,下列说法正确的是( )
A.对称轴是直线 ![]() ,最小值是
,最小值是 ![]()
B.对称轴是直线 ![]() ,最大值是
,最大值是 ![]()
C.对称轴是直线 ![]() ,最小值是
,最小值是 ![]()
D.对称轴是直线 ![]() ,最大值是
,最大值是 ![]()
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】观察:从2开始,连续的偶数相加,它们的和的情况如下图:

(1)当加数m的个数为n时,和(S)与n之间有什么样的数量关系,用公式表示出来;
(2)按此规律计算(写出必要的演算过程):
①2+4+6+…+300的值;
②162+164+166+…+400的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简再求值:当a=9时,求a+![]() 的值,甲乙两人的解答如下:
的值,甲乙两人的解答如下:
甲的解答为:原式=a+![]() =a+(1-a)=1.
=a+(1-a)=1.
乙的解答为:原式=a+![]() =a+(a-1)=2a-1=17.
=a+(a-1)=2a-1=17.
两种解答中,_____的解答是错误的,错误的原因是当a=9时______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个![]() 的方格棋盘的
的方格棋盘的![]() 格里放了一枚棋子,如果规定棋子每步只能向上、向下或向左、向右走一格,那么这枚棋子走如下的步数后能到达
格里放了一枚棋子,如果规定棋子每步只能向上、向下或向左、向右走一格,那么这枚棋子走如下的步数后能到达![]() 格的是( ).
格的是( ).

A. 7 B. 14 C. 21 D. 28
查看答案和解析>>
科目:初中数学 来源: 题型:
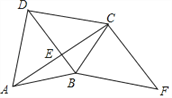
【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.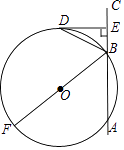
(1)求证:直线DE是⊙O的切线;
(2)若 BF=10,sin∠BDE= ![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(理解新知)
如图①,已知![]() ,在
,在![]() 内部画射线
内部画射线![]() ,得到三个角,分别为
,得到三个角,分别为![]() 、
、![]() 、
、![]() ,若这三个角中有一个角是另外一个角的2倍,则称射线
,若这三个角中有一个角是另外一个角的2倍,则称射线![]() 为
为![]() 的“2倍角线”
的“2倍角线”
(1)角的平分线 这个角的“2倍角线”;(填“是”或“不是”)
(2)若![]() ,射线
,射线![]() 为
为![]() 的“2倍角线”,则
的“2倍角线”,则![]()
![]() ;
;
(解决问题)
如图②,已知![]() ,射线
,射线![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 的速度绕
的速度绕![]() 点逆时针旋转:射线
点逆时针旋转:射线![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 的速度绕
的速度绕![]() 点顺时针旋转,射线
点顺时针旋转,射线![]() 、
、![]() 同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为
同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为![]() .
.
(3)当射线![]() 、
、![]() 旋转到同一条直线上时,求
旋转到同一条直线上时,求![]() 的值;
的值;
(4)若![]() 、
、![]() 、
、![]() 三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的
三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的![]() 的值.(本题中所研究的角都是小于等于
的值.(本题中所研究的角都是小于等于![]() 的角.)
的角.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=6,N为AB上一点,且AN=2,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM,MN,则BM+MN的最小值是( )
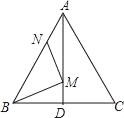
A. 8 B. 10 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
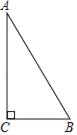
【题目】如图,在Rt△ABC中,∠C=90°,AC=4.
(1)若BC=2,求AB的长;
(2)若BC=a,AB=c,求代数式(c﹣2)2﹣(a+4)2+4(c+2a+3)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com