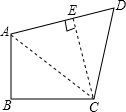
解:连接AC,过点C作CE⊥AD于E
∵AB=3,BC=4,∠B=90°
∴AC=

=5.
又∵CD=5,AD=6
∴AE=3
∴EC=

=4.
∴S
四边形=S
△ABC+S
△ACD=

×3×4+

×6×4
=6+12
=18.
分析:连接AC,过点C作CE⊥AD于E,利用勾股定理分别计算出AE和EC的长,然后求出△ABC和△ACD的面积即可.
点评:此题主要考查学生对勾股定理和三角形面积的理解和掌握,解答此题的关键是连接AC,过点C作CE⊥AD于E正好把该四边形分成△ABC和△ACD,然后根据三角形的面积公式计算就可以了.

