
”¾ĢāÄæ”æČēĶ¼1£¬µć![]() ”¢
Ӣ![]() Ӣ
Ӣ![]() Ӣ
”¢![]() ·Ö±šŌŚ¾ŲŠĪ
·Ö±šŌŚ¾ŲŠĪ![]() µÄ±ß
µÄ±ß![]() ”¢
Ӣ![]() Ӣ
Ӣ![]() Ӣ
”¢![]() ÉĻ£¬
ÉĻ£¬![]() .
.
ĒóÖ¤£ŗ![]() .(
.(![]() ±ķŹ¾Ć껿)
±ķŹ¾Ć껿)

ŹµŃéĢ½¾æ£ŗ
ijŹżŃ§ŹµŃ銔×é·¢ĻÖ£ŗČōĶ¼1ÖŠ![]() £¬µć
£¬µć![]() ŌŚ
ŌŚ![]() ÉĻŅĘ¶ÆŹ±£¬ÉĻŹö½įĀŪ»į·¢Éś±ä»Æ£¬·Ö±š¹żµć
ÉĻŅĘ¶ÆŹ±£¬ÉĻŹö½įĀŪ»į·¢Éś±ä»Æ£¬·Ö±š¹żµć![]() ”¢
”¢![]() ×÷
×÷![]() ±ßµÄĘ½ŠŠĻߣ¬ŌŁ·Ö±š¹żµć
±ßµÄĘ½ŠŠĻߣ¬ŌŁ·Ö±š¹żµć![]() ”¢
”¢![]() ×÷
×÷![]() ±ßµÄĘ½ŠŠĻߣ¬ĖÄĢõĘ½ŠŠĻß·Ö±šĻą½»ÓŚµć
±ßµÄĘ½ŠŠĻߣ¬ĖÄĢõĘ½ŠŠĻß·Ö±šĻą½»ÓŚµć![]() ”¢
Ӣ![]() Ӣ
Ӣ![]() Ӣ
”¢![]() £¬µĆµ½¾ŲŠĪ
£¬µĆµ½¾ŲŠĪ![]() .
.
ČēĶ¼2£¬µ±![]() Ź±£¬Čō½«µć
Ź±£¬Čō½«µć![]() Ļņµć
Ļņµć![]() ææ½ü(
ææ½ü(![]() )£¬¾¹żĢ½Ė÷£¬·¢ĻÖ£ŗ
)£¬¾¹żĢ½Ė÷£¬·¢ĻÖ£ŗ
![]() .
.
ČēĶ¼3£¬µ±![]() Ź±£¬Čō½«µć
Ź±£¬Čō½«µć![]() Ļņµć
Ļņµć![]() ææ½ü(
ææ½ü(![]() £¬ĒėĢ½Ė÷
£¬ĒėĢ½Ė÷![]() ”¢
”¢![]() Óė
Óė![]() Ö®¼äµÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ.
Ö®¼äµÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ.

ĒØŅĘÓ¦ÓĆ£ŗ
ĒėÖ±½ÓÓ¦ÓĆ”°ŹµŃéĢ½¾æ”±ÖŠ·¢ĻֵĽįĀŪ½ā“šĻĀĮŠĪŹĢā.
(1)ČēĶ¼4£¬µć![]() ”¢
Ӣ![]() Ӣ
Ӣ![]() Ӣ
”¢![]() ·Ö±šŹĒĆ껿ĪŖ25µÄÕż·½ŠĪ
·Ö±šŹĒĆ껿ĪŖ25µÄÕż·½ŠĪ![]() ø÷±ßÉĻµÄµć£¬ŅŃÖŖ
ø÷±ßÉĻµÄµć£¬ŅŃÖŖ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬Ēó
£¬Ēó![]() µÄ³¤.
µÄ³¤.

(2)ČēĶ¼5£¬ŌŚ¾ŲŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬µć
£¬µć![]() ”¢
”¢![]() ·Ö±šŌŚ±ß
·Ö±šŌŚ±ß![]() ”¢
”¢![]() ÉĻ£¬
ÉĻ£¬![]() £¬
£¬![]() £¬µć
£¬µć![]() ”¢
”¢![]() ·Ö±šŹĒ±ß
·Ö±šŹĒ±ß![]() ”¢
”¢![]() ÉĻµÄ¶Æµć£¬ĒŅ
ÉĻµÄ¶Æµć£¬ĒŅ![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ”¢
”¢![]() £¬ĒėÖ±½ÓŠ“³öĖıߊĪ
£¬ĒėÖ±½ÓŠ“³öĖıߊĪ![]() Ć껿µÄ×ī“óÖµ.
Ć껿µÄ×ī“óÖµ.

”¾“š°ø”æĪŹĢā³ŹĻÖ£ŗ![]() £»ŹµŃéĢ½¾æ£ŗ
£»ŹµŃéĢ½¾æ£ŗ![]() £»ĒØŅĘÓ¦ÓĆ£ŗ£Ø1£©
£»ĒØŅĘÓ¦ÓĆ£ŗ£Ø1£©![]() £»£Ø2£©
£»£Ø2£©![]()
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗĪŹĢā³ŹĻÖ£ŗøł¾Ż¾ŲŠĪµÄŠŌÖŹ£¬Ķعżøī²¹·ØĄūÓĆČż½ĒŠĪµÄĆ껿ŗĶ¾ŲŠĪµÄĆ껿æɵƵ½½įĀŪ£»
ŹµŃéĢ½¾æ£ŗÓÉĢāŅāµĆ£¬µ±½«µć![]() Ļņµć
Ļņµć![]() ææ½ü
ææ½ü![]() Ź±£¬Ķعżøī²¹·ØĄūÓĆČż½ĒŠĪµÄĆ껿ŗĶ¾ŲŠĪµÄĆ껿æɵƵ½½įĀŪ£»
Ź±£¬Ķعżøī²¹·ØĄūÓĆČż½ĒŠĪµÄĆ껿ŗĶ¾ŲŠĪµÄĆ껿æɵƵ½½įĀŪ£»
ĒØŅĘÓ¦ÓĆ£ŗ£Ø1£©ÓÉÉĻĆęµÄ½įĀŪ£¬½įŗĻĶ¼ŠĪ£¬Ķعżøī²¹·ØĄūÓĆČż½ĒŠĪµÄĆ껿ŗĶ¾ŲŠĪµÄĆ껿æɵƵ½½įĀŪ£»
£Ø2£©Ö±½Óøł¾Ż¹ęĀÉŠ“³ö½į¹ū¼“æÉ.
ŹŌĢā½āĪö£ŗĪŹĢā³ŹĻÖ£ŗ
ŅņĪŖĖıߊĪ![]() ŹĒ¾ŲŠĪ£¬ĖłŅŌ
ŹĒ¾ŲŠĪ£¬ĖłŅŌ![]() £¬
£¬![]() £¬
£¬
ÓÖŅņĪŖ![]() £¬ĖłŅŌĖıߊĪ
£¬ĖłŅŌĖıߊĪ![]() ŹĒ¾ŲŠĪ£¬
ŹĒ¾ŲŠĪ£¬
ĖłŅŌ![]() £¬Ķ¬ĄķæɵĆ
£¬Ķ¬ĄķæɵĆ![]() .
.
ŅņĪŖ![]() £¬ĖłŅŌ
£¬ĖłŅŌ![]() .
.
ŹµŃéĢ½¾æ£ŗ
ÓÉĢāŅāµĆ£¬µ±½«µć![]() Ļņµć
Ļņµć![]() ææ½ü
ææ½ü![]() Ź±£¬
Ź±£¬
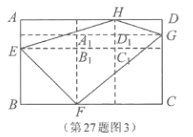
ČēĶ¼ĖłŹ¾£¬![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬![]() £¬
£¬
ĖłŅŌ![]() £¬
£¬
ĖłŅŌ![]() £¬
£¬
¼“![]() .
.
ĒØŅĘÓ¦ÓĆ£ŗ
(1) ČēĶ¼ĖłŹ¾£¬ÓÉ”°ŹµŃéĢ½¾æ”±µÄ½įĀŪæÉÖŖ![]() £¬
£¬
ĖłŅŌ![]() £¬
£¬
ŅņĪŖÕż·½ŠĪĆ껿ŹĒ25£¬ĖłŅŌ±ß³¤ĪŖ5£¬
ÓÖ![]() £¬
£¬
ĖłŅŌ![]() £¬
£¬![]() £¬
£¬
ĖłŅŌ![]() £¬
£¬
ĖłŅŌ£¬![]() .
.
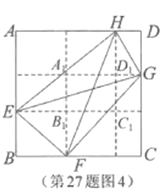
£Ø2£©ĖıߊĪ![]() Ć껿µÄ×ī“óÖµĪŖ
Ć껿µÄ×ī“óÖµĪŖ![]() .
.


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĶ¼ŠĪÖŠ£¬ŹĒÖį¶Ō³ĘĶ¼ŠĪ¶ų²»ŹĒÖŠŠÄ¶Ō³ĘĶ¼ŠĪµÄŹĒ£Ø””””£©
A.Ō²B.µČŃüČż½ĒŠĪC.Ę½ŠŠĖıߊĪD.ĢŻŠĪ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÅ×ĪļĻßy=©2x2ĻČĻņÓŅĘ½ŅĘ1øöµ„Ī»£¬ŌŁĻņĻĀĘ½ŅĘ2øöµ„Ī»£¬ĖłµĆÅ×ĪļĻߵĽāĪöŹ½ŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōA£Ø0£¬y1£©£¬B£Ø©3£¬y2£©£¬C£Ø3£¬y3£©ĪŖ¶ž“ĪŗÆŹży=©x2+4x©kµÄĶ¼ĻóÉĻµÄČżµć£¬Ōņy1£¬y2£¬y3µÄ“󊔹ŲĻµŹĒ£Ø””””£©
A.y1£¼y2£¼y3B.y2£¼y1£¼y3C.y3£¼y1£¼y2D.y1£¼y3£¼y2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬¹żµć
ÖŠ£¬¹żµć![]() µÄÖ±Ļß½»
µÄÖ±Ļß½»![]() ÖįÕż°ėÖįÓŚµć
ÖįÕż°ėÖįÓŚµć![]() £¬½«Ö±Ļß
£¬½«Ö±Ļß![]() ČĘ×ŵć
ČĘ×ŵć![]() Ė³Ź±ÕėŠż×Ŗ
Ė³Ź±ÕėŠż×Ŗ![]() ŗ󣬷ֱšÓė
ŗ󣬷ֱšÓė![]() Öį
Öį![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() ”¢
Ӣ![]() .
.
(1)Čō![]() £¬ĒóÖ±Ļß
£¬ĒóÖ±Ļß![]() µÄŗÆŹż¹ŲĻµŹ½£»
µÄŗÆŹż¹ŲĻµŹ½£»
(2)Į¬½Ó![]() £¬Čō
£¬Čō![]() µÄĆ껿ŹĒ5£¬Ēóµć
µÄĆ껿ŹĒ5£¬Ēóµć![]() µÄŌĖ¶ÆĀ·¾¶³¤.
µÄŌĖ¶ÆĀ·¾¶³¤.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĻŲĻģÓ¦”°½ØÉč»·±£½ŚŌ¼ŠĶÉē»į”±µÄŗÅÕŁ£¬¾ö¶Ø׏֜²æ·Ö“åÕņŠŽ½ØŅ»ÅśÕÓĘų³Ų£¬Ź¹Å©ĆńÓƵ½¾¼Ć”¢»·±£µÄÕÓĘųÄÜŌ“£®ŠŅø£“å¹²ÓŠ264»§“åĆń£¬Õžø®²¹Öś“åĄļ34ĶņŌŖ£¬²»×ć²æ·ÖÓÉ“åĆń¼Æ׏£®ŠŽ½ØAŠĶ”¢BŠĶÕÓĘų³Ų¹²20øö£®Į½ÖÖŠĶŗÅÕÓĘų³ŲĆæøöŠŽ½Ø·ŃÓĆ”¢æɹ©Ź¹ÓĆ»§Źż”¢ŠŽ½ØÓƵŲĒéæöČēĻĀ±ķ£ŗ
ÕÓĘų³Ų | ŠŽ½Ø·ŃÓĆ£ØĶņŌŖ/øö£© | æɹ©Ź¹ÓĆ»§Źż£Ø»§/øö£© | Õ¼µŲĆ껿£Øm2/øö£© |
AŠĶ | 3 | 20 | 48 |
BŠĶ | 2 | 3 | 6 |
Õžø®Ļą¹Ų²æĆÅÅśøųøĆ“åÕÓĘų³ŲŠŽ½ØÓƵŲ708Ę½·½Ć×£®É芎½ØAŠĶÕÓĘų³Ųxøö£¬ŠŽ½ØĮ½ÖÖŠĶŗÅÕÓĘų³Ų¹²Šč·ŃÓĆyĶņŌŖ£®
£Ø1£©ÓĆŗ¬ÓŠxµÄ“śŹżŹ½±ķŹ¾y£»
£Ø2£©²»³¬¹żÕžø®ÅśøųŠŽ½ØÕÓĘų³ŲÓƵŲĆ껿£¬ÓÖŅŖŹ¹øĆ“åĆ滧“åĆńÓĆÉĻÕÓĘųµÄŠŽ½Ø·½°øÓŠ¼øÖÖ£»
£Ø3£©ČōĘ½¾łĆ滧“åĆń¼Æ׏700ŌŖ£¬ÄÜ·ńĀś×ćĖłŠč·ŃÓĆ×īÉŁµÄŠŽ½Ø·½°ø£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōa=©0.22 £¬ b=©2©2 £¬ c=£Ø© ![]() £©©2 £¬ d=£Ø©
£©©2 £¬ d=£Ø© ![]() £©0 £¬ ½«a£¬b£¬c£¬d°““ӓ󵽊”µÄ¹ŲĻµÅÅĮŠ £®
£©0 £¬ ½«a£¬b£¬c£¬d°““ӓ󵽊”µÄ¹ŲĻµÅÅĮŠ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
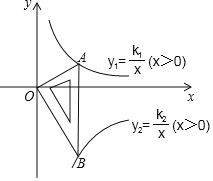
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾ŹĒŅ»æéŗ¬30”ć£¬60”ć£¬90”ćµÄÖ±½ĒČż½Ē°å£¬Ö±½Ē¶„µćOĪ»ÓŚ×ų±źŌµć£¬Š±±ßAB“¹Ö±ÓŚxÖį£¬¶„µćAŌŚŗÆŹży1=![]() £Øx£¾0£©µÄĶ¼ĻóÉĻ£¬¶„µćBŌŚŗÆŹży2=
£Øx£¾0£©µÄĶ¼ĻóÉĻ£¬¶„µćBŌŚŗÆŹży2=![]() £Øx£¾0£©µÄĶ¼ĻóÉĻ£¬”ĻABO=30”ć£¬Ōņ
£Øx£¾0£©µÄĶ¼ĻóÉĻ£¬”ĻABO=30”ć£¬Ōņ![]() = £®
= £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼,Ō²ÖłŠĪČŻĘ÷ÖŠ£¬øßĪŖ120cm£¬µ×ĆęÖܳ¤ĪŖ100cm£¬ŌŚČŻĘ÷ÄŚ±ŚĄėČŻĘ÷µ×²æ40cm£¬µÄµćB“¦ÓŠŅ»ĪĆ×Ó,“ĖŹ±Ņ»Ö»±Ś»¢ÕżŗĆŌŚČŻĘ÷Ķā±Ś,ĄėČŻĘ÷ÉĻŃŲ40cmÓėĪĆ×ÓĻą¶ŌµÄµćA“¦£¬
Ōņ±Ś»¢²¶×½ĪĆ×ÓµÄ×ī¶Ģ¾ąĄėĪŖCm£ØČŻĘ÷ŗńāŃŗöĀŌ²»¼Ę£©.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com