
【题目】问题探究
(1)如图①,在正方形ABCD内,请画出使∠BPC=90°的所有点P;
(2)如图②,已知矩形ABCD,AB=9,BC=10,在矩形ABCD内(含边)画出使∠BPC=60°的所有点P,并求出△APD面积的最大值;
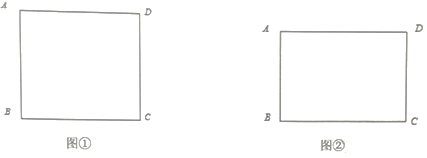
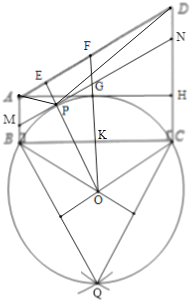
(3)随着社会发展,农业观光园走进了我们的生活,某农业观光园的平面示意图如图3所示的四边形ABCD,其中∠A=120°,∠B=∠C=90°,AB=![]() km,BC=6km,观光园的设计者想在园中找一点P,使得点P与点A、B、C、D所连接的线段将整个观光园分成四个区域,用来进行不同的设计与规划,从实用和美观的角度他们还要求在△BPC的区域内∠BPC=120°,且△APD的区域面积最小,试问在四边形ABCD内是否存在这样的点P,使得∠BPC=120°,且△APD面积最小?若存在,请你在图中画出点P点的位置,并求出△APD的最小面积.若不存在,说明理由.
km,BC=6km,观光园的设计者想在园中找一点P,使得点P与点A、B、C、D所连接的线段将整个观光园分成四个区域,用来进行不同的设计与规划,从实用和美观的角度他们还要求在△BPC的区域内∠BPC=120°,且△APD的区域面积最小,试问在四边形ABCD内是否存在这样的点P,使得∠BPC=120°,且△APD面积最小?若存在,请你在图中画出点P点的位置,并求出△APD的最小面积.若不存在,说明理由.
【答案】(1)见解析;(2)45-![]() ;(3)9
;(3)9![]() -12.
-12.
【解析】
(1)如图,以BC为直径作上半圆(不含点B、C),根据直径所对的圆周角为直角得到该半圆上的任意一点即可;(2)以BC为边作等边△BPC;作等边△BPC的外接圆⊙O与AB交于F,与AD交于点E、G,与CD交于点H,![]() 和
和![]() 即为所求,(3)以BC为边向下作等边△BCQ,作△BCQ的外接圆⊙O,则劣弧BC即为所求,作AD的平行线MN切劣弧BC于P,连接OP并延长交AD于E,由切线的性质可得OP⊥MN,即可证明OP⊥AD,由平行线间垂线段最短,可得三角形APD面积最小,过A作AH⊥CD于H,由BC=10可得△BCQ的外接圆半径为2
即为所求,(3)以BC为边向下作等边△BCQ,作△BCQ的外接圆⊙O,则劣弧BC即为所求,作AD的平行线MN切劣弧BC于P,连接OP并延长交AD于E,由切线的性质可得OP⊥MN,即可证明OP⊥AD,由平行线间垂线段最短,可得三角形APD面积最小,过A作AH⊥CD于H,由BC=10可得△BCQ的外接圆半径为2![]() ,与BC弦的弦心距为
,与BC弦的弦心距为![]() ,根据AB=
,根据AB=![]() 可得AH与⊙O相切,切点为G,根据平行线的判定定理可得OC//AD,进而可证明四边形OCDF为平行四边形,即可证明CD=OF,根据直角三角形锐角互余的关系可得∠EOF=30°,通过解直角三角形可求出OE的长,进而可求出PE的长,根据三角形面积公式即可得答案.
可得AH与⊙O相切,切点为G,根据平行线的判定定理可得OC//AD,进而可证明四边形OCDF为平行四边形,即可证明CD=OF,根据直角三角形锐角互余的关系可得∠EOF=30°,通过解直角三角形可求出OE的长,进而可求出PE的长,根据三角形面积公式即可得答案.
(1)如图,以BC为直径作上半圆(不含点B、C),
∵直径所对的圆周角是90°,
∴![]() (不含点B、C)即为所求.
(不含点B、C)即为所求.
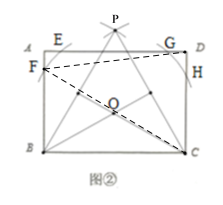
(2)以BC为边作等边△BPC;作等边△BPC的外接圆⊙O与AB交于F,与AD交于点E、G,与CD交于点H,
∵△BPC是等边三角形,![]() 和
和![]() 是弦BC所对圆周角,
是弦BC所对圆周角,
∴![]() 和
和![]() 即为所求.
即为所求.
连接CF,DF,
∵三角形的底相等,高越大面积越大,
∴当P点与F点或H点重合时面积最大,
∵∠BFC=60°,BC=10,
∴tan60°=![]() =
=![]() =
=![]() ,
,
∴BF=![]() ,
,
∴AF=9-![]() ,
,
∴S△AFD=![]() ×(9-
×(9-![]() )×10=45-
)×10=45-![]() .
.
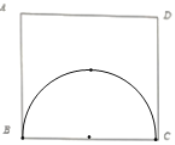
(3)如图,以BC为边向下作等边△BCQ,作△BCQ的外接圆⊙O,则劣弧BC即为所求,作AD的平行线MN切劣弧BC于P,连接OP并延长交AD于E,
∴OP⊥MN,
∵AD//MN,
∴OE⊥AD,
∵平行线间垂线段最短,
∴△APD面积最小,
过A作AH⊥CD于H,作OK⊥BC,延长OK交AH于G,交AD于F,
∵△BCQ是等边三角形,
∴∠OBC=30°,BK=3,
∴OB=![]() =
=![]() ,OK=
,OK=![]() =
=![]() ,即外接圆的半径为
,即外接圆的半径为![]() ,BC的弦心距为
,BC的弦心距为![]() ,
,
∵∠DCB=90°,
∴AH//BC,
∴OG⊥AH,
∴AB=KG=CH,
∵AB=![]() ,
,
∴OG=OK+KG=OK+AB=2![]() =OB,
=OB,
∴AH与⊙O相切,切点为G,
∵∠D=60°,∠OCD=90°+30°=120°,
∴AD//OC,
∵∠OKC=∠DCK=90°,
∴OF//CD,
∴四边形OCDF是平行四边形,
∴OF=CD,
∵∠BAD=120°,∠BAH=90°,
∴∠FAG=30°,
∵∠FAG+∠AFO=90°,∠EOF+∠AFO=90°,
∴∠EOF=∠FAG=30°,
∵∠FAG=30°,AH=BC=6,
∴AD=![]() =
=![]() ,HD=6
,HD=6![]() tan30°=2
tan30°=2![]() ,
,
∴OF=CD=HD+CH=2![]() +
+![]() =3
=3![]() ,
,
∴OE=OF![]() cos∠EOF=OF
cos∠EOF=OF![]() cos30°=3
cos30°=3![]() ×
×![]() =
=![]() ,
,
∴PE=OE-OP=![]() -2
-2![]() ,
,
∴S△APD=![]() AD
AD![]() PE=
PE=![]() ×(
×(![]() -2
-2![]() )×
)×![]() =9
=9![]() -12.
-12.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
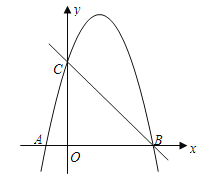
(1)求抛物线的解析式;
(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标;
(3)在(2)的条件下,连接BD,点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
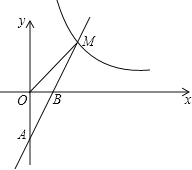
【题目】如图,一次函数![]() 的图象经过
的图象经过![]() ,
,![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象在第一象限内的交点为
的图象在第一象限内的交点为![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 在x轴上是否存在点P,使
在x轴上是否存在点P,使![]() ?若存在,求出点P的坐标;若不存在,说明理由.
?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
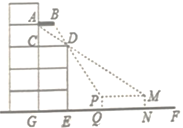
【题目】周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳蓬的宽度,如图,由于无法直接测量,小凯便在楼前面的地面上选择了一条直线EF,通过在直线EF上选点观测,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳蓬A点处:当他位于Q点时,视线从P点通过露台D点正好落在遮阳蓬B点处,这样观测到两个点A,B间的距离即为遮阳蓬的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、PQ、MN均为垂直于EF,MN=PQ,露台的宽CD=GE,测得GE=5米,EN=13.2米,QN=6.2,请你根据以上信息,求出遮阳蓬的宽AB是多少米?(结果精确到0.01米)
查看答案和解析>>
科目:初中数学 来源: 题型:
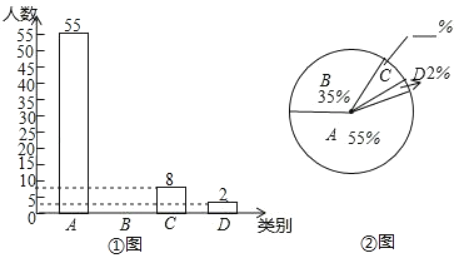
【题目】我省某地区为了了解2017年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.读重点高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图(如①图,如②图)
(1)该地区共调查了_____名九年级学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该地区2017年初中毕业生共有4000人,请估计该地区今年初中毕业生中读重点高中的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )

A.①② B.①④ C.①③④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
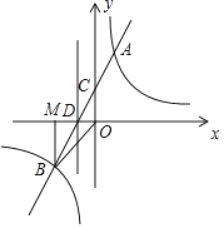
【题目】如图,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A,B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为点M,BM=OM=2,点A的纵坐标为4.
(k≠0)的图象交于第一、三象限内的A,B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为点M,BM=OM=2,点A的纵坐标为4.
(1)求该反比例函数和一次函数的表达式;
(2)直线AB交x轴于点D,过点D作直线l⊥x轴,如果直线l上存在点P,坐标平面内存在点Q.使四边形OPAQ是矩形,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com