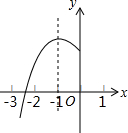Question

2．如图，抛物线y=ax²+bx+c（a≠0）的对称轴为x=-1，与x轴的一个交点在（-3，0）和（-2，0）之间，其部分图象如图所示，则下列结论：
（1）b²-4ac＞0；
（2）2a=b；
（3）点（-$\frac{7}{2}$，y₁）、（-$\frac{3}{2}$，y₂）、（$\frac{5}{4}$，y₃）是该抛物线上的点，则y₁＜y₂＜y₃；
（4）3b+2c＜0；
（5）t（at+b）≤a-b（t为任意实数）．
其中正确结论的个数是（　　）

• A． 2
• B． 3
• C． 4
• D． 5

Answer 1

分析 逐一分析5条结论是否正确：（1）由抛物线与x轴有两个不相同的交点结合根的判别式即可得出该结论正确；（2）根据抛物线的对称轴为x=-1，即可得出b=2a，即（2）正确；（3）根据抛物线的对称性找出点（-$\frac{13}{4}$，y₃）在抛物线上，再结合抛物线对称轴左边的单调性即可得出（3）错误；（4）由x=-3时，y＜0，即可得出3a+c＜0，结合b=2a即可得出（4）正确；（5）由方程at²+bt+a=0中△=b²-4a•a=0结合a＜0，即可得出抛物线y=at²+bt+a中y≤0，由此即可得出（5）正确．综上即可得出结论．

解答 解：（1）由函数图象可知，抛物线与x轴有两个不同的交点，
∴关于x的方程ax²+bx+c=0有两个不相等的实数根，
∴△=b²-4ac＞0，
∴（1）正确；
（2）∵抛物线y=ax²+bx+c（a≠0）的对称轴为x=-1，
∴-$\frac{b}{2a}$=-1，
∴2a=b，
∴（2）正确；
（3）∵抛物线的对称轴为x=-1，点（$\frac{5}{4}$，y₃）在抛物线上，
∴（-$\frac{13}{4}$，y₃）．
∵-$\frac{7}{2}$＜-$\frac{13}{4}$＜-$\frac{3}{2}$，且抛物线对称轴左边图象y值随x的增大而增大，
∴y₁＜y₃＜y₂．
∴（3）错误；
（4）∵当x=-3时，y=9a-3b+c＜0，且b=2a，
∴9a-3×2a+c=3a+c＜0，
∴6a+2c=3b+2c＜0，
∴（4）正确；
（5）∵b=2a，
∴方程at²+bt+a=0中△=b²-4a•a=0，
∴抛物线y=at²+bt+a与x轴只有一个交点，
∵图中抛物线开口向下，
∴a＜0，
∴y=at²+bt+a≤0，
即at²+bt≤-a=a-b．
∴（5）正确．
故选C．

点评 本题考查了二次函数图象与系数的关系、二次函数与不等式以及抛物线与x轴的交点，解题的关键是逐一分析5条结论是否正确．本题属于中档题，难度不大，解决该题型题目时，熟练掌握二次函数的图象是关键．