
 请根据图编写一道题,并给出解答.
请根据图编写一道题,并给出解答. 分析 根据函数图象找出问题,再根据图形中点的坐标利用待定系数法求出函数解析式.
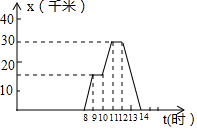
解答 小明早上八点骑车到离家30km的游乐场游玩,14时返回家中,如图是离家距离x(千米)关于时间t(时)的函数图象,求出x关于t的函数关系式.
解:设x关于t的函数关系式为x=kt+b,
当8≤t≤9时,将(8,0)、(9,15)代入x=kt+b,
$\left\{\begin{array}{l}{8k+b=0}\\{9k+b=15}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=15}\\{b=-120}\end{array}\right.$,
∴此时x=15t-120;
当9≤t≤10时,x=15;
当10≤t≤11时,将(10,15)、(11,30)代入x=kt+b,
$\left\{\begin{array}{l}{10k+b=15}\\{11k+b=30}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=15}\\{b=-135}\end{array}\right.$,
∴此时x=15t-135;
当11≤t≤12时,x=30;
当12≤t≤14时,将(12,30)、(14,0)代入x=kt+b,
$\left\{\begin{array}{l}{12k+b=30}\\{14k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-15}\\{b=210}\end{array}\right.$,
∴此时x=-15t+210.
综上所述:x=$\left\{\begin{array}{l}{15t-120(8≤t≤9)}\\{15(9≤t≤10)}\\{15t-135(10≤t≤11)}\\{30(11≤t≤12)}\\{-15t+210(12≤t≤14)}\end{array}\right.$.
点评 本题考查了函数图象以及待定系数法求一次函数解析式,根据点的坐标利用待定系数法求出一次函数解析式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
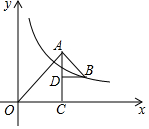 如图,点C在x轴的正半釉上,且∠ACO=90°,CO=CA,点D在边AC上,在边AC的右侧取一点B,使∠ADB=90°,且BD=DA,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若S△OAC-S△BAD=5k-2,则k的值为$\frac{4}{9}$.
如图,点C在x轴的正半釉上,且∠ACO=90°,CO=CA,点D在边AC上,在边AC的右侧取一点B,使∠ADB=90°,且BD=DA,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若S△OAC-S△BAD=5k-2,则k的值为$\frac{4}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
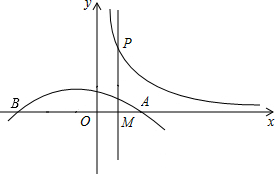 如图,抛物线L:y=-$\frac{1}{2}$(x-1)(x+3)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=8.
如图,抛物线L:y=-$\frac{1}{2}$(x-1)(x+3)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
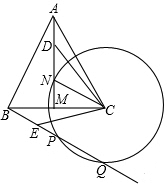 如图,在等边△ABC中,已知AB=8cm,线段AM为BC边上的中线.点N在线段AM上,且MN=3cm,动点D在直线AM上运动,连接CD,△CBE是由△CAD旋转得到的.以点C为圆心,以CN为半径作⊙C与直线BE相交于点P,Q两点.
如图,在等边△ABC中,已知AB=8cm,线段AM为BC边上的中线.点N在线段AM上,且MN=3cm,动点D在直线AM上运动,连接CD,△CBE是由△CAD旋转得到的.以点C为圆心,以CN为半径作⊙C与直线BE相交于点P,Q两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,AG⊥BC,EF=$\sqrt{3}$,求AG的长.
如图,在?ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,AG⊥BC,EF=$\sqrt{3}$,求AG的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com