
 如图,如图正方形ABCD内一点E,满足△CDE为正三角形,直线AE交BC于F点,过E点的直线GH⊥AF,交AB于点G,交CD于点H.以下结论:
如图,如图正方形ABCD内一点E,满足△CDE为正三角形,直线AE交BC于F点,过E点的直线GH⊥AF,交AB于点G,交CD于点H.以下结论:| 2 |
| AE |
| EH |
| 2 |
| 3 |
| AE |
| EH |
| 1 |
| 2 |
|

| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| AE |
| EH |
| EF |
| EH |
| ||||
|
| ||
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 答案直接填写在后面的横线上
答案直接填写在后面的横线上查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省泰州市海陵区八年级下学期期中考试数学试卷(带解析) 题型:解答题
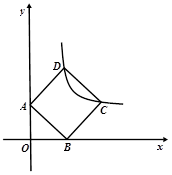
如图1,在平面直角坐标系中,点A、C分别在 轴、
轴、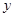 轴上,四边形OABC是面积为4的正方形,函数
轴上,四边形OABC是面积为4的正方形,函数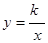 (
( >0)的图象经过点B.
>0)的图象经过点B.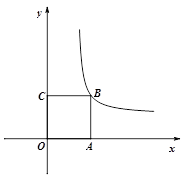
(1)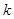 = ;
= ;
(2)如图2,将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′和正方形MA′BC.设线段MC′、NA′分别与函数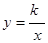 (
( >0)的图象交于点E、F,则点E、F的坐标分别为:E ( , ) ,F ( , );
>0)的图象交于点E、F,则点E、F的坐标分别为:E ( , ) ,F ( , );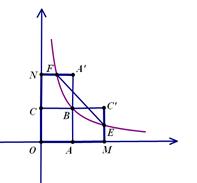
(3)如图3,面积为4的正方形ABCD的顶点A、B分别在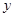 轴、
轴、 轴上,顶点C、D在反比例函数
轴上,顶点C、D在反比例函数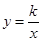 (
( >0)的图像上,试求OA、OB的长。(请写出必要的解题过程)
>0)的图像上,试求OA、OB的长。(请写出必要的解题过程)

查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建龙岩永定仙师中学九年级上学期第三次月考数学试卷(解析版) 题型:解答题
某数学兴趣小组开展了一次课外活动,过程如下:如图,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.
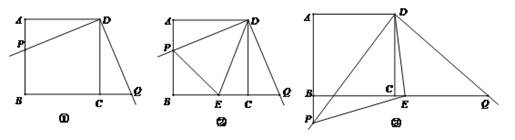
(1)求证:DP=DQ;
(2)如图,小明在图①的基础上做∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)如图,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com