
 轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为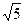 ,过点C作⊙A的切线交
,过点C作⊙A的切线交 轴于点B(-4,0).
轴于点B(-4,0).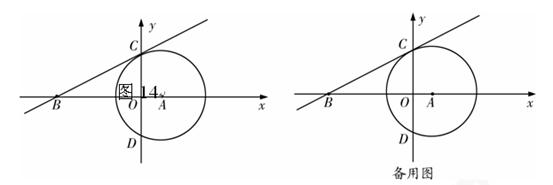
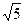

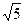 ,OA="1" ,则OC=2
,OA="1" ,则OC=2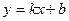 ,它过点C(0,2),B(?4,0),则有
,它过点C(0,2),B(?4,0),则有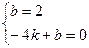 解之得
解之得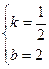
 ……………………….(2分)
……………………….(2分) 轴,
轴,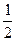 a + 2
a + 2 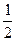 ×1200=600 ……………………….(3分)
×1200=600 ……………………….(3分)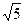
 ∴AG =
∴AG =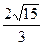 ……………………….(4分)
……………………….(4分)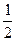 a+ 2
a+ 2 
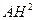 +
+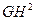 =
=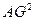
 +
+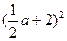 =
=
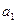 =
= ,
,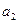 = ?
= ? (舍去) ……………………….(5分)
(舍去) ……………………….(5分)  ,
, + 2 ) ……………………….(6分) 解析:
+ 2 ) ……………………….(6分) 解析:

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
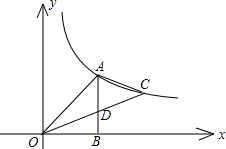 象交于点A、C,连接OA、OC,过点A作AB⊥x轴于点B,交OC于点D,且△AOB为等腰直角三角形,tan∠COB=
象交于点A、C,连接OA、OC,过点A作AB⊥x轴于点B,交OC于点D,且△AOB为等腰直角三角形,tan∠COB=| 1 | 4 |
查看答案和解析>>
科目:初中数学 来源:2007年德州市初中毕业、升学统一考试数学试卷 题型:044
已知:如图14,在△ABC中,D为AB边上一点,∠A=36°,AC=BC,AC2=AB·AD.
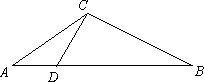
(1)试说明:△ADC和△BDC都是等腰三角形;
(2)若AB=1,求AC的值;
(3)请你构造一个等腰梯形,使得该梯形连同它的两条对角线得到8个等腰三角形.(标明各角的度数)
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图14,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,点
,点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)写出直线![]() 的解析式.
的解析式.
(2)求![]() 的面积.
的面积.
 (3)若点
(3)若点![]() 在线段
在线段![]() 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从![]() 向
向![]() 运动(不与
运动(不与![]() 重合),同时,点
重合),同时,点![]() 在射线
在射线![]() 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从![]() 向
向![]() 运动.设运动时间为
运动.设运动时间为![]() 秒,请写出
秒,请写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并求出点
的函数关系式,并求出点![]() 运动多少时间时,
运动多少时间时,![]() 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源:2011年北京市通州区中考二模数学试卷 题型:解答题
已知:如图14,⊙A与 轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为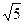 ,过点C作⊙A的切线交
,过点C作⊙A的切线交 轴于点B(-4,0)
轴于点B(-4,0) .
.
(1)求切线BC的解析式;
(2)若点P是第一象限内⊙A上的一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点G的坐标.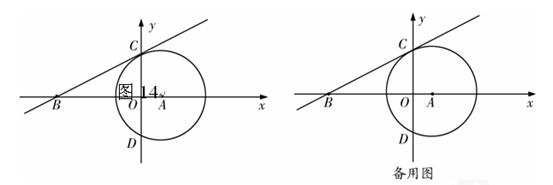
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com