解:(1)∵AD⊥BC,
∴∠ADC=90°,即△ADC为直角三角形,
又F为斜边AC的中点,
∴AF=CF=DF=

AC,
∴∠FDC=∠C,又∠C=70°
∴∠FDC=∠C=70°,
又∠AFD为△FDC的外角,
∴∠AFD=∠FDC+∠C=140°;
(2)当△ABC满足AB=AC时,四边形AEDF为菱形,理由如下:
证明:∵AB=AC,且AD⊥BC,
∴D为BC的中点,又F为AC的中点,
∴DF为△ABC的中位线,
∴DF=

AB,DF∥AB,
又E为AB的中点,∴AE=

AB,
∴DF=AE,且DF∥AE,
∴四边形AEDF为平行四边形,
同理DE为△ABC的中位线,
∴DE=

AC,又AB=AC,
∴DE=DF,
则四边形AEDF为菱形;
(3)△ABC需满足AB=AC,再加上∠BAC=90°,可使四边形AEDF为正方形,理由如下:
证明:∵AB=AC,且AD⊥BC,
∴D为BC的中点,又F为AC的中点,
∴DF为△ABC的中位线,
∴DF=

AB,DF∥AB,
又E为AB的中点,∴AE=

AB,
∴DF=AE,且DF∥AE,
∴四边形AEDF为平行四边形,
同理DE为△ABC的中位线,
∴DE=

AC,又AB=AC,
∴DE=DF,
∴四边形AEDF为菱形,
又∠BAC=90°,
∴四边形AEDF为正方形.
分析:(1)由AD垂直于BC,根据垂直定义得到∠ADC=90°,即三角形ADC为直角三角形,又F为AC的中点,根据斜边上的中线等于斜边的一半,可得DF等于AC的一半,再根据中点定义得到AF与CF相等,且都等于AC的一半,等量代换可得DF=CF,根据等边对等角得到∠FDC=∠C,由∠C的度数求出∠FDC的度数,由∠AFD为三角形FDC的外角,根据外角性质即可求出所求角的度数;
(2)三角形ABC满足AB=AC时,四边形AEDF为菱形,理由为:由AB=AC,且AD与BC垂直,根据三线合一得到D为BC的中点,又F为中点,可得DF为三角形ABC的中位线,可得DF与AB平行,且等于AB的一半,又AE也为AB的一半,等量代换可得AE=DF,又AE与DF平行,根据一组对边平行且相等的四边形为平行四边形,再由DE也为三角形ABC的中位线,可得ED等于AC的一半,由AB=AC,等量代换可得DE=DF,根据邻边相等的平行四边形为菱形可得AEDF为菱形;
(3)由第二问三角形ABC满足AB=AC,得到AEDF为菱形,再加上∠BAC=90°,根据有一个角为直角的菱形为正方形可得AEDF为正方形.
点评:此题考查了直角三角形斜边上的中线等于斜边的一半,三角形的中位线定理,平行四边形、菱形及正方形的判定,以及三角形的外角性质,属于条件探究型题,解答此类题应采用“逆向思维”,视结论为题设,寻求必要条件,往往缺少的就是那个条件.

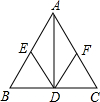 如图,在△ABC中,AD⊥BC,垂足为D,E、F分别是AB、AC的中点.
如图,在△ABC中,AD⊥BC,垂足为D,E、F分别是AB、AC的中点. AC,
AC, AB,DF∥AB,
AB,DF∥AB, AB,
AB, AC,又AB=AC,
AC,又AB=AC, AB,DF∥AB,
AB,DF∥AB, AB,
AB, AC,又AB=AC,
AC,又AB=AC,

 阅读快车系列答案
阅读快车系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为