
����Ŀ���ۺ���̽��
��ͼ1��ƽ��ֱ������ϵ�У�������y=ax2+bx+3��x��ֱ��ڵ�A����2��0����B��4��0������y�ύ�ڵ�C����D��y�Ḻ������һ�㣬ֱ��BD��������y=ax2+bx+3�ڵ��������ڵ�E����4��y����F��������y=ax2+bx+3�ϵ�һ�㣬�ҵ�F��ֱ��BE�Ϸ�������F��ƽ����x���ֱ������ƽ��m����λ���Ⱥ�ǡ������ֱ��BE�ϵĵ�G����
��1����������y=ax2+bx+3�ı���ʽ�������E�����ꣻ
��2�����F�ĺ�����Ϊx����4��x��4��������������⣺
�ٵ���G���D�غ�ʱ����ƽ�ƾ���m��ֵ��
���ú�x��ʽ�ӱ�ʾƽ�ƾ���m������m�����ֵ��
��3����ͼ2������F��x��Ĵ���FP����ֱ��BE�ڵ�P������ΪF������FD���Ƿ���ڵ�F��ʹ��FDP����FDG�������Ϊ1��2�������ڣ�ֱ��д����F�����ꣻ�������ڣ�˵�����ɣ�

���𰸡���1������4����6������2����![]() -1����8����3����������
-1����8����3����������
��������
��1���Ƚ�A����2��0����B��4��0��������y=ax2+bx+3���a��b��ֵ������������ߵı���ʽ���ٽ�E������������ʽ���y��ֵ���ɣ�
��2������ֱ��BD�ı���ʽΪy=kx+b����B��4��0����E����4����6���������k��b��ֵ���ٽ�x=0�������ʽ���D�����꣬����G���D�غ�ʱ���ɵ�G�����꣬GF��x�ᣬ�ʿɵ�F�������꣬ �ٽ�y=��3���������ߵĽ���ʽ���ɵõ�F�����꣬�ٸ���m=FG���ɵ�m��ֵ��
�����F���G�����꣬����m=FG�г����̻���ɵó�m�Ķ��κ�����ϵʽ���ٸ��ݶ��κ�����ͼ��ɵ�m��ȡֵ��Χ��
��3���ֱ��������F��x������ʱ���Ҳ�ʱ�����������������FDP����FDG�������Ϊ1��2����PD��DG=1��2����֪FP��HD����FH��HG=1��2���ٷֱ����F,G������꣬�ٸ��������ϵ�г���ʽ������⼴�ɵ�F������.
�⣺��1����A����2��0����B��4��0��������y=ax2+bx+3�ã�![]() ����ã�
����ã�![]() ��
��
�������ߵı���ʽΪy=��![]() x2+
x2+![]() x+3��
x+3��
��E����4��y������ã�y=��6��
���E����������4����6����
��2������ֱ��BD�ı���ʽΪy=kx+b����B��4��0����E����4����6������ã�![]() ��
��
��ã�![]() ��
��
��ֱ��BD�ı���ʽΪy=![]() x��3��
x��3��
��x=0����y=![]() x��3�ã�y=��3��
x��3�ã�y=��3��
��D��0����3����
����G���D�غ�ʱ��G������Ϊ��0����3����
��GF��x�ᣬ
��F����������3��
��y=��3���������ߵĽ���ʽ�ã���![]() x2+
x2+![]() x+3=��3��
x+3=��3��
��ã�x=![]() +1��x=��
+1��x=��![]() +1��
+1��
����4��x��4��
���F����������![]() +1����3����
+1����3����
��m=FG=![]() ��1��
��1��
�����F��������x����![]() x2+
x2+![]() x+3�������G��������x+m��
x+3�������G��������x+m��![]() ��x+m����3����
��x+m����3����
����![]() x2+
x2+![]() x+3=
x+3=![]() ��x+m����3������ã�m=��
��x+m����3������ã�m=��![]() x2+8��
x2+8��
����![]() ��0��
��0��
��m�����ֵ��
��x=0ʱ��m�����ֵΪ8��
��3������F��x������ʱ������ͼ��ʾ��
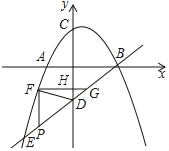
�ߡ�FDP����FDG�������Ϊ1��2��
��PD��DG=1��2��
��FP��HD��
��FH��HG=1��2��
��F��������x����![]() x2+
x2+![]() x+3�������G����������2x����
x+3�������G����������2x����![]() x��3����
x��3����
����![]() x2+
x2+![]() x+3=��
x+3=��![]() x��3�������ã�x2��6x��16=0��
x��3�������ã�x2��6x��16=0��
��ã�x=��2��x=8����ȥ����
���F����������2��0����
����F��x����Ҳ�ʱ������ͼ��ʾ��
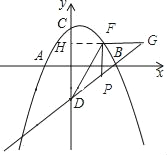
�ߡ�FDP����FDG�������Ϊ1��2��
��PD��DG=1��1��
��FP��HD��
��FH��HG=1��1��
��F��������x����![]() x2+
x2+![]() x+3�������G��������2x��
x+3�������G��������2x��![]() x��3����
x��3����
����![]() x2+
x2+![]() x+3=
x+3=![]() x��3�������ã�x2+2x��16=0��
x��3�������ã�x2+2x��16=0��
��ã�x=![]() ��1��x=��
��1��x=��![]() ��1����ȥ����
��1����ȥ����
���F��������![]() ��1��
��1��![]() ����
����
������������F����������2��0����![]() ��1��
��1��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y��kx��3��ͼ����A���Һ���ֵy��x��������������A�����겻�����ǣ�������
A.����2����4��B.����1��2��C.��5��1��D.����1����4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC��BD�ཻ�ڵ�O����DAB����CBA������������һ���������Բ���ʹ��ADB�ա�CBA���ǣ�������

A.AD��BCB.��ABD����BACC.OA��OBD.AC��BD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����ABD���ǵȱ������Σ���E��F�ֱ���BC��AC�ϣ�BE��CF��AE��BF���ڵ�G��

��1�����AGF�Ķ�����
��2������DG����AG��3��BG��2����DG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �������㣬����
�������㣬����![]() ��
��![]() ��Ϊ�෴��.��
��Ϊ�෴��.��![]() �ǵڶ�������һ�㣬��
�ǵڶ�������һ�㣬��![]() ����
����![]() ��ֱ��
��ֱ��![]() ��һ���㣻
��һ���㣻
��1����![]() ����
����![]() �ǵ��������Σ���
�ǵ��������Σ���![]() �Ķ�����
�Ķ�����
��2����![]() ��ֱ��
��ֱ��![]() ���˶������У���
���˶������У���![]() ���ʱ����
���ʱ����![]() �Ĵ�С.
�Ĵ�С.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ͼ��ӳ���ǣ�С���Ӽ����ܲ�ȥ�������������������һ������ߵ��ľߵ�ȥ��ʣ�Ȼ��ɢ���ؼң�����x��ʾʱ�䣬y��ʾС����ҵľ��룮
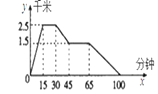
����ͼ��ش��������⣺
��1����������С���Ҷ�Զ��С���Ӽҵ����������˶���ʱ�䣿
��2�����������ľߵ��Զ��
��3��С�����ľߵ궺���˶���ʱ�䣿
��4��С�����ľߵ�ؼҵ�ƽ���ٶ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������ABCD����������A��2����1����C��6��2������MΪy����һ�㣬��MAB�����Ϊ6�������������⣺
��1������B�������� ����
��2������BD����BD�ij���
��3����ֱ��д����M�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱߡ�ABC����
��1����ͼ1��P��Q��BC���ϵ����㣬AP=AQ����BAP=20�㣬���AQB�Ķ�����
��2����P��Q��BC���ϵ��������㣨�����B��C�غϣ�����P�ڵ�Q����࣬��AP=AQ����Q����ֱ��AC�ĶԳƵ�ΪM������AM��PM��
�������⽫ͼ2��ȫ��
��С��ͨ���۲졢ʵ��������룺�ڵ�P��Q�˶��Ĺ����У�ʼ����PA=PM��С������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1��Ҫ֤��PA=PM��ֻ��֤��APM�ǵȱ������Σ�
�뷨2����BA��ȡһ��N��ʹ��BN=BP��Ҫ֤��PA=PM��ֻ��֤��ANP�ա�PCM��
�뷨3�����߶�BP�Ƶ�B˳ʱ����ת60�㣬�õ��߶�BK��Ҫ֤PA=PM��ֻ��֤PA=CK��PM=CK��
����ο�������뷨������С��֤��PA=PM��һ�ַ������ɣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2��bx��c(a��b��cΪ��������a��0)�е�x��y�IJ��ֶ�Ӧֵ���±���
x | ��1 | 0 | 1 | 3 |
y | ��1 | 3 | 5 | 3 |
���н��ۣ���c��3���ڵ�x��1ʱ��y��ֵ��x���������С���ۺ��������ֵ��5����abc��0.������ȷ����(����)
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com