
【题目】如图,在平面直角坐标系中,![]() 的三个顶点都在格点上,点
的三个顶点都在格点上,点![]() 的坐标为
的坐标为![]() .
.
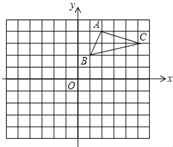
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ,并写出点
,并写出点![]() 的坐标
的坐标![]() .
.
(2)画出![]() 绕原点
绕原点![]() 旋转后
旋转后![]() 得到的
得到的![]() ,并写出
,并写出![]() 点的坐标
点的坐标![]() .
.
(3)![]() 是否为直角三角形?答 (填是或者不是).
是否为直角三角形?答 (填是或者不是).
(4)利用格点图,画出![]() 边上的高
边上的高![]() ,并求出
,并求出![]() 的长,
的长,![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】有一批共享单车需要维修,维修后继续投放骑用,现有甲、乙两人做维修,甲每天维修16辆,乙每天维修的车辆比甲多8辆,甲单独维修完成这批共享单车比乙单独维修完多用20天,公司每天付甲80元维修费,付乙120元维修费.
(1)问需要维修的这批共享单车共有多少辆?
(2)在维修过程中,公司要派一名人员进行质量监督,公司负担他每天10元补助费,现有三种维修方案:①由甲单独维修;
②由乙单独维修;
③甲、乙合作同时维修,你认为哪种方案最省钱,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
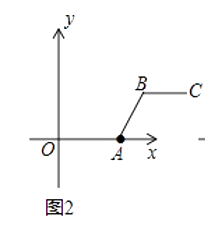
【题目】定义:P、Q分别是两条线段a,b上任意一点,线段PQ长度的最小值叫做线段a与线段b的距离.已知,O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离为;当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为;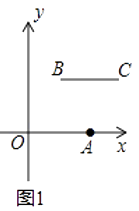
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.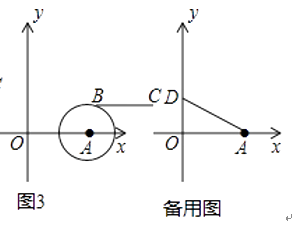
(3)当m值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,点D(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m值,使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
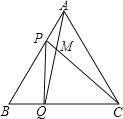
【题目】点P、Q分别是边长为4cm的等边![]() 的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是
的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是![]() ,设运动时间为t秒.
,设运动时间为t秒.
![]() 连接AQ、CP交于点M,则在P、Q运动的过程中,
连接AQ、CP交于点M,则在P、Q运动的过程中,![]() 变化吗:若变化,则说明理由,若不变,则求出它的度数;
变化吗:若变化,则说明理由,若不变,则求出它的度数;
![]() 连接PQ,
连接PQ,
![]() 当
当![]() 秒时,判断
秒时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 当
当![]() 时,则
时,则![]() ______秒
______秒![]() 直接写出结果
直接写出结果![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们通常用作差法比较代数式大小.例如:已知M=2x+3,N=2x+1,比较M和N的大小.先求M﹣N,若M﹣N>0,则M>N;若M﹣N<0,则M<N;若M﹣N=0,则M=N,反之亦成立.本题中因为MN=2x+3(2x+1)=2>0,所以M>N.
(1)如图1是边长为a的正方形,将正方形一边不变,另一边增加4,得到如图2所示的新长方形,此长方形的面积为S1;将图1中正方形边长增加2得到如图3所示的新正方形,此正方形的面积为S2.用含a的代数式表示S1= ,S2= (需要化简).然后请用作差法比较S1与S2大小;
(2)已知A=2a2﹣6a+1,B=a2﹣4a﹣1,请你用作差法比较A与B大小.
(3)若M=(a﹣4)2,N=16﹣(a﹣6)2,且M=N,求(a﹣4)(a﹣6)的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.
求:(1)折叠后DE的长;(2)以折痕EF为边的正方形面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com