Question

19．如图，在△ABC中，∠ABC=90°，AB=BC，点D是△ABC内部一点，连接AD，BD和CD．
（1）如图1，若∠BDC=90°，BD=1，CD=2，求AC的长．
（2）如图2，若CD平分∠ACB，∠BDC=90°，过点B作BE∥AC交AD的延长线于点E，求证：AD=DE．
（3）如图3，若CD=CB，∠BCD=30°，取线段AC的中点F，连接DF，求证：∠AFD=45°

Answer 1

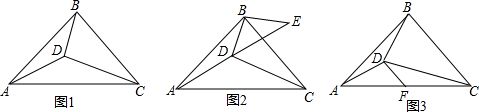
分析 （1）如图1，先根据勾股定理求BC的长，再根据勾股定理求AC的长；
（2）如图2，作辅助线，构建全等三角形，证明△BDC≌△PDC，得BD=PD，再证明△BDE≌△PDA，得结论；
（3）作辅助线，构建等边三角形DBE，证明△CEB≌△CED，得∠BCE=15°，再证明△ABD≌△CBE，
得∠BAD=15°，则∠BAD=∠ABD，所以AD=BD，证明△ADF≌△BDF，得DF平分∠AFB，从而得出结论．

解答 解：（1）如图1，∵∠BDC=90°，BD=1，CD=2，
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，
∵AB=BC=$\sqrt{5}$，
由勾股定理得：AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{5+5}$=$\sqrt{10}$；
（2）如图2，延长BD交AC于P，
∵DC平分∠ACB，
∴∠BCD=∠ACD，
∵∠BDC=90°，
∴∠BDC=∠PDC=90°，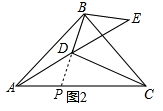
∵CD=CD，
∴△BDC≌△PDC，
∴BD=PD，
∵BE∥AC，
∴∠E=∠EAC，∠EBD=∠DPA，
∴△BDE≌△PDA，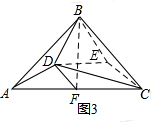
∴AD=DE；
（3）如图3，以BD为边作等边三角形BDE，连接BF、CE，
∴BD=DE=BE，
∵AB=BC，F是AC的中点，
∴BF⊥AC，
∴∠AFB=90°，
∵∠ABC=90°，
∴BF=AF，
∵CD=BC，∠BCD=30°，
∴∠CBD=∠CDB=75°，
∵CE=CE，
∴△CEB≌△CED，
∴∠BCE=∠DCE=15°，
∵∠CBD=75°，∠DBE=60°，
∴∠CBE=75°-60°=15°，
∵∠ABC=90°，
∴∠ABD=90°-75°=15°，
∴∠ABD=∠CBE，
∴△ABD≌△CBE，
∴∠BAD=∠BCE=15°，
∴∠ABD=∠BAD=15°，
∴AD=BD，
∵DF=DF，
∴△ADF≌△BDF，
∴∠AFD=∠BFD=$\frac{1}{2}$∠AFB=$\frac{1}{2}$×90°=45°．

点评 本题是三角形的综合题，考查了全等三角形、等边三角形、等腰三角形、勾股定理等性质，需要的知识点较多，做好本题要熟练掌握以下几点：①如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a²+b²=c²；②等腰直角三角形中，两直角边相等，且每个锐角等于45°，斜边是直角边的$\sqrt{2}$倍；③等边三角形的各边相等且各角为60°；④等腰三角形的底边上的高、底边上的中线、顶角的平分线互相重合；此题的第三问还可以连接BF交CD于G，证明△BDF∽△CGB得出结论．