练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，完成下面推理过程

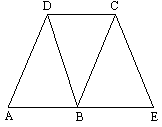
    (1)由∠ABD＝∠BDC(已知)，可得________∥________根据________________

    (2)由∠DBC＝∠ADB(已知)，可得________∥________根据________________

    (3)由∠CBE＝∠DCB(已知)，可得________∥________根据________________

    (4)由∠CBE＝∠A(已知)，可得________∥________根据________________

    (5)由∠A＋∠ADC＝，可得________∥________根据________________

    (6)由∠A＋∠ABC＝，可得________∥________根据________________

    (7)由________________，可得DB∥CE(同位角相等，两直线平行)；

    (8)由________________，可得DB∥CE(内错角相等，两直线平行)；

    (9)由________________，可得DB∥CE(同旁内角互补，两直线平行)．

    答案：
    解析：

    　　(1)DC,AE,内错角相等，两直线平行

    　　(2)AD,BC,内错角相等，两直线平行

    　　(3)DC,AE,内错角相等，两直线平行

    　　(4)AD,BC,同位角相等，两直线平行

    　　(5)DC,AE,同旁内角互补，两直线平行

    　　(6)AD,BC,同旁内角互补，两直线平行

    　　(7)∠ABD＝∠E

    　　(8)∠CBD＝∠BCE

    　　(9)∠E＋∠DBE＝


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    29、如图，已知点D、E为△ABC的边BC上两点．AD=AE，BD=CE，为了判断∠B与∠C的大小关系，请你填空完成下面的推理过程，并在空白括号内注明推理的依据．
    解：过点A作AH⊥BC，垂足为H．
    ∵在△ADE中，AD=AE（已知）
    AH⊥BC（所作）
    ∴DH=EH（等腰三角形底边上的高也是底边上的中线）
    又∵BD=CE（已知）
    ∴BD+DH=CE+EH（等式的性质）
    即：BH=
    CH

    又∵
    AH⊥BC
    （所作）
    ∴AH为线段
    BC
    的垂直平分线
    ∴AB=AC（线段垂直平分线上的点到线段两个端点的距离相等）
    ∴
    ∠B=∠C
    （等边对等角）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    仔细想一想，完成下面的推理过程 如图，已知∠BED=∠B+∠D，试说明AB与CD的关系．
    解：AB∥CD，理由如下：
    过点E作∠BEF=∠B
    ∴AB∥
    EF
    EF
    （
    内错角相等，两直线平行
    内错角相等，两直线平行
    ）
    ∵∠BED=∠B+∠D（
    已知
    已知
    ）
    ∴
    ∠DEF
    ∠DEF
    =∠D （
    等量代换
    等量代换
    ）
    ∴
    CD
    CD
    ∥EF （
    内错角相等，两直线平行
    内错角相等，两直线平行
    ）
    ∴AB∥CD（
    平行于同一条直线的两条直线平行
    平行于同一条直线的两条直线平行
    ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

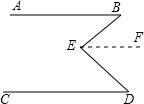    仔细想一想，完成下面的推理过程 如图，已知∠BED=∠B+∠D，试说明AB与CD的关系．
    解：AB∥CD，理由如下：
    过点E作∠BEF=∠B
    ∴AB∥________（________）
    ∵∠BED=∠B+∠D（________）
    ∴________=∠D （________）
    ∴________∥EF （________）
    ∴AB∥CD（________）

    查看答案和解析>>

    科目：初中数学 来源：重庆市月考题 题型：解答题

    仔细想一想，完成下面的推理过程 如图，已知∠BED=∠B+∠D，试说明AB与CD的关系。
    解：AB∥CD，理由如下：
    过点E作∠BEF=∠B，
    ∴AB∥ _________ （ _________ ）
    ∵∠BED=∠B+∠D（ _________ ）
    ∴__________=∠D（__________）
    ∴__________∥EF（_________）
    ∴AB∥CD（_________）。

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，已知点D、E为△ABC的边BC上两点．AD=AE，BD=CE，为了判断∠B与∠C的大小关系，请你填空完成下面的推理过程，并在空白括号内注明推理的依据．
    精英家教网

    过点A作AH⊥BC，垂足为H．
    ∵在△ADE中，AD=AE（已知）
    AH⊥BC（所作）
    ∴DH=EH（等腰三角形底边上的高也是底边上的中线）
    又∵BD=CE（已知）
    ∴BD+DH=CE+EH（等式的性质）
    即：BH=______
    又∵______（所作）
    ∴AH为线段______的垂直平分线
    ∴AB=AC（线段垂直平分线上的点到线段两个端点的距离相等）
    ∴______（等边对等角）

    查看答案和解析>>

    同步练习册答案