试题分析:(1)解一元二次方程,求得OA、OB的长,证△AOC∽△COB,推出OC
2=OA•OB,即可得出答案。
解x
2﹣25x+144=0得x=9或x=16,
∵OA、OB的长分别是一元二次方程x
2﹣25x+144=0的两个根(OA<OB),
∴OA=9,OB=16。
在Rt△AOC中,∠CAB+∠ACO=90°,
在Rt△ABC中,∠CAB+∠CBA=90°,
∴∠ACO=∠CBA。
∵∠AOC=∠COB=90°,∴△AOC∽△COB。∴OC
2=OA•OB。∴OC=12,
∴C(0,12)。
(2)应用相似三角形求得点D 的坐标,应用待定系数法即可求得直线AD的解析式。
在Rt△AOC和Rt△BOC中,∵OA=9,OC=12,OB=16,∴AC=15,BC=20。
∵DE⊥AB,∴∠ACD=∠AED=90°。
又∵AD平分∠CAB,AD=AD,∴△ACD≌△AED。∴AE=AC=15。
∴OE=AE﹣OA=15﹣9=6,BE=10。
∵∠DBE=∠ABC,∠DEB=∠ACB=90°,∴△BDE∽△BAC。
∴

,即

,解得

。
∴D(6,

)。
设直线AD的解析式是y=kx+b,
将A(﹣9,0)和D(6,

)代入得:

,解得
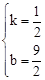
。
∴直线AD的解析式是:

。
(3)存在点M,使得C、B、N、M为顶点的四边形是正方形。
① 以BC为对角线时,作BC的垂直平分线交BC于Q,交x轴于F,在直线FQ上取一点M,使∠CMB=90°,则符合此条件的点有两个,
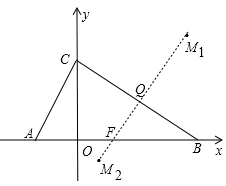
BQ=CQ=

BC=10,
∵∠BQF=∠BOC=90°,∠QBF=∠CBO,
∴△BQF∽△BOC。∴

。
∵BQ=10,OB=16,BC=20,∴BF=

。
∴OF=16﹣

=

。∴F(

,0)。
∵OC=12,OB=16,Q为BC中点,∴Q(8,6)。
设直线QF的解析式是y=ax+c,
代入得:
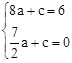
,解得

。
∴直线FQ的解析式是:

。
设M的坐标是(x,

),
根据CM=BM和勾股定理得:(x﹣0)
2+(

﹣12)
2=(x﹣16)
2+(

﹣0)
2,
解得x
1=14,x
2=2。
∴M的坐标是(14,14),(2,﹣2)。
②以BC为一边时,过B作BM
3⊥BC,且BM
3=BC=20,过M
3Q⊥OB于Q,还有一点M
4,CM
4=BC=20,CM
4⊥BC,
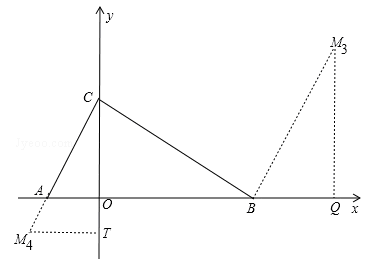
则∠COB=∠M
3B=∠CBM
3=90°。
∴∠BCO+∠CBO=90°,
∠CBO+∠M
3BQ=90°。
∴∠BCO=∠M
3BQ。
∵在△BCO和△M
3BQ中,

,
∴△BCO≌△M
3BQ(AAS)。
∴BQ=CO=12,QM
3=OB=16,
OQ=16+12=28,
∴M
3的坐标是(28,16)。
同法可求出CT=OB=16,M
4T=OC=12,OT=16﹣12=4,
∴M
4的坐标是(﹣12,﹣4)。
综上所述,存在点M,使得C、B、N、M为顶点的四边形是正方形,
点M的坐标是(28,16)或(14,14)或(﹣12,﹣4)或(2,﹣2)。


 。
。 ,即
,即 ,解得
,解得 。
。 )。
)。 )代入得:
)代入得: ,解得
,解得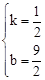 。
。 。
。
 BC=10,
BC=10, 。
。 。
。 =
= 。∴F(
。∴F( ,0)。
,0)。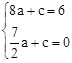 ,解得
,解得 。
。 。
。 ),
), ﹣12)2=(x﹣16)2+(
﹣12)2=(x﹣16)2+( ﹣0)2,
﹣0)2,
 ,
,

 ,x2+6x﹣27=0,x2+4x+4=0,都是“偶系二次方程”.
,x2+6x﹣27=0,x2+4x+4=0,都是“偶系二次方程”.