
如图13,14,已知四边形ABCD为正方形,在射线AC上有一动点P,作PE⊥AD(或延长线)于E,作PF⊥DC(或延长线)于F,作射线BP交EF于G.
(1)在图13中,设正方形ABCD的边长为2, 四边形ABFE的面积为y, AP=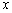 ,求y关于
,求y关于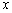 的函数表达式.
的函数表达式.
(2)结论GB⊥EF对图13,图14都是成立的,请任选一图形给出证明;
(3)请根据图14证明:△FGC∽△PFB.
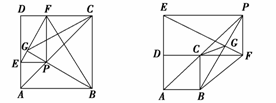
图13 图14
解:(1)∵EP AD,PF
AD,PF DC,∴四边形EPFD是矩形,
DC,∴四边形EPFD是矩形,
∵AP=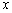 ,
,
∴AE=EP=DF=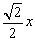 ,
,
 ,
,
∴


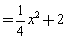
(2)在图13中证明GB⊥EF.
①证法一:延长FP交AB于H,
∵PF⊥DC,PE⊥AD,∴PF⊥PE,PH⊥HB,
即∠BHP=90°
∴在Rt△FPE与Rt△BHP中
因 ABCD是正方形,
∴易知PF=FC=HB,EP=PH
∴Rt△FPE≌Rt△BHP
∴∠PFE=∠PBH,
又∠FPG=∠BPH,
∴△FPG∽ △BPH,
∴∠FGP=∠BHP=90°,即GB⊥EF
分析: 要GB⊥EF,只要∠5 +∠3=90°,而∠5 +∠4=90°,只要证∠3=∠4,
而∠2 =∠3, ,只要证∠4=∠2,而∠4=∠1,故只要∠1=∠2.
证法二: 如答案图13-2,连接PD,延长FP交AB于H,
延长EP交BC于M,
易知DC=BC, ∠DCP=∠BCP=45°,PC=PC,
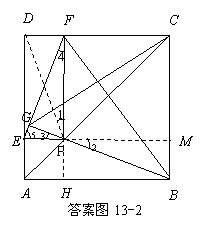 ∴△DPC≌△BP
∴△DPC≌△BP C
C
∴∠DPC=∠BPC,即∠1+45°=45°+∠2,
∴∠1=∠2,
 而∠1=∠4, ∠2 =∠3,
而∠1=∠4, ∠2 =∠3,
∴∠3=∠4,
而∠5 +∠4=90°,∴∠5 +∠3=90°,
∴∠PGE=180°-(∠5 +∠3)=90°,
即GB⊥EF.
注:在图14中证法与上面类似.
(3)证法一:
∵GB⊥EF,∴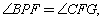 …①…
…①…
连接PD,在△DPC和△BPC中
∵DC=BC, ∠DCP=∠BCP =135°,PC=PC,
=135°,PC=PC,
∴ △DPC≌△BPC,∴PD=PB.
而PD=EF, ∴EF=PB.
又∵GB⊥EF,∴
∴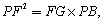
而PF=FC, ∴
∴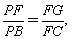 ………②
………②
∴由①②得△FGC∽△PFB.
证法二:
∵GB⊥EF,∴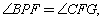 ………①
………①
又∵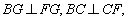
取BF的中点M,则有:

∴B,C,G,F四点在以M为圆心,MB为 半径的圆上.
半径的圆上.
∴ ………②
………②
∴由①②得△FGC∽△PFB.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
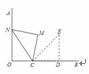
如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 的值为( )
的值为( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如题22-1图和题22-2图所示的不完整的统计图。
 |
(1) 这次被调查的同学共有 名;
(2) 把条形统计图(题22-1图)补充完整;
(3) 校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐。据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
2014年5月12日,国家统计局公布了《2013年农民工监测调查报告》,报告显示:我国农民工收入持续快速增长.某地区农民工人均月收入增长率如图7所示,并将人均月收入绘制成如图8所示的不完整的条形统计图.
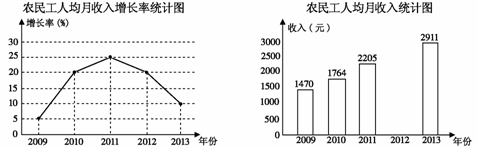
图7 图8
根据以上统计图解答下列问题:
(1)2013年农民工人均月收入的增长率是多少?
(2)2011年农民工人均月收入是多少?
(3)小明看了统计图后说:“农民工2012年的人均月收入比2011年的少了.”你认为小明的说法正确吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com