
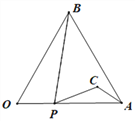
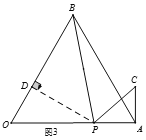
【题目】如图,等边△AOB的边长为4,点P从点O出发,沿OA以每秒1个单位的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA.在点P从O向A运动的过程中,当△PCA为直角三角形时t的值为___________.
【答案】2或![]()
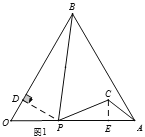
【解析】如图(1)过点P作PD⊥OB于点D,过C作CE⊥OA于E,∴∠PDO=∠PEC=90°,
∵∠O=60°,∴∠OPD=30°,∴OD=![]() t,∴BD=4-
t,∴BD=4-![]() t,PD=
t,PD=![]() t,
t,
∵线段BP的中点绕点P按顺时针方向旋转60°得点C,
∴∠BPC=60°,BP=2PC,∵∠OPD=30°,
∴∠BPD+∠CPE=90°,∴∠DBP=∠CPE,
∴△PCE∽△BPD,
∴![]() ,
,
∴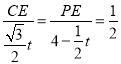 ,
,
∴CE=![]() t,PE=2-
t,PE=2-![]() t,OE=2+
t,OE=2+![]() t,
t,
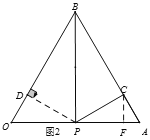
如图(2)当∠PCA=90度时,作CF⊥PA,∴△PCF∽△ACF,∴△PCF∽△ACF,∴![]() ,∴CF2=PFAF,
,∴CF2=PFAF,
∵PF=2-![]() t,AF=4-OF=2-
t,AF=4-OF=2-![]() t, CF=
t, CF=![]() t,
t,
∴(![]() t)2=(2-
t)2=(2-![]() t)(=2-
t)(=2-![]() t),
t),
∴t=2,这时P是OA的中点;
如图(3)当∠CAP=90°时,此时OA=OE,
∴2+![]() t=4,∴t=
t=4,∴t=![]() ,
,
故答案为:2或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么,最多可购买多少件甲种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两城间的铁路路程为1600千米,经过技术改造,列车实施了提速,提速后比提速前速度增加了20千米/小时,列车从甲城到乙城行驶时间减少4小时,这条铁路在现有条件下安全行驶速度不得超过140千米/小时,请你用学过的知识说明在这条铁路的现有条件下列车是否还可以再提速。
查看答案和解析>>
科目:初中数学 来源: 题型:
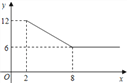
【题目】某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图;B类杨梅深加工后再销售,深加工总费用s(万元)与加工数量t(吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
(1)A类杨梅的销售量为5吨时,它的平均销售价格是每吨多少万元?
(2)若该公司收购10吨杨梅,其中A类杨梅有4吨,则经营这批杨梅所获得的毛利润(w)为多少万元?(毛利润=销售总收入﹣经营总成本)
(3)若该公司收购20吨杨梅,要使该公司获得30万元毛利润,求直销的A类杨梅有多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比学习:一动点沿着数轴先向右平移3个单位长度,再向左平移2个单位长度,相当于向右平移1个单位长度.用实数加法表示为3+(-2)=1.若坐标平面上的点有如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位长度),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位长度),则把有序数对{a,b}叫做这一平移的“平移量”,“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2},{1,2}+{3,1}.
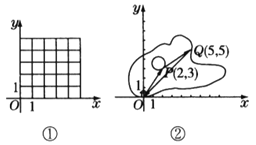
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到点A,再按照“平移量”{1,2}平移到点B;若先把动点P按照“平移量”{1,2}平移到点C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图①中画出四边形OABC.
(3)如图②所示,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
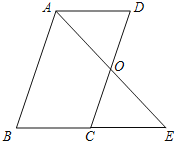
【题目】已知:如图,□ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
![]() 求证:
求证: ![]() ≌
≌![]() ;
;
![]() 连接
连接![]() ,当
,当![]() ______°和
______°和![]() ______°时,四边形ACED是正方形?请说明理由.
______°时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com