
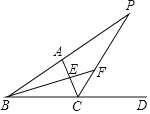
【题目】如图,已知BE是△ABC的角平分线,CP是△ABC的外角∠ACD的平分线.延长BE,BA分别交CP于点F,P.
(1)求证:∠BFC![]() ∠BAC;
∠BAC;
(2)小智同学探究后提出等式:∠BAC=∠ABC+∠P.请通过推理演算判断“小智发现”是否正确?
(3)若2∠BEC﹣∠P=180°,求∠ACB的度数.
【答案】(1)证明见解析;(2)“小智发现”是错误的,证明见解析;(3)∠ACB=60°.
【解析】
(1)根据角平分线的定义得到∠PCD=![]() ∠ACD,∠FBC=
∠ACD,∠FBC=![]() ∠ABC,根据三角形的外角的性质即可证明结论;
∠ABC,根据三角形的外角的性质即可证明结论;
(2)根据(1)中的结论变形后可得结论;
(3)根据三角形的外角和角平分线的定义,综合已知,等量代换可得结论.
(1)∵CP是∠ACD的平分线,
∴∠PCD![]() ∠ACD.
∠ACD.
∵BF是∠ABC的平分线,
∴∠FBC![]() ∠ABC,
∠ABC,
∴∠BFC=∠PCD﹣∠FBC![]() (∠ACD﹣∠ABC)
(∠ACD﹣∠ABC)![]() ∠BAC;
∠BAC;
(2)由(1)知∠BFC![]() ∠BAC,
∠BAC,
∴∠BAC=2∠BFC=2×(![]() ∠ABC+∠P)=∠ABC+2∠P,
∠ABC+∠P)=∠ABC+2∠P,
∴“小智发现”是错误的;
(3)△ABE中,∠BEC=∠ABE+∠BAC![]() ∠ABC+∠BAC,
∠ABC+∠BAC,
△ACP中,∠BAC=∠ACP+∠P,
∴∠BEC![]() ∠ABC+∠ACP+∠P
∠ABC+∠ACP+∠P![]() ∠ABC+∠PCD+∠P.
∠ABC+∠PCD+∠P.
∵∠PCD![]() ∠ABC+∠BFC,
∠ABC+∠BFC,
∴∠BEC![]() ∠ABC+∠P
∠ABC+∠P![]() ∠ABC
∠ABC![]() ∠BAC=∠ABC+∠P
∠BAC=∠ABC+∠P![]() ∠BAC.
∠BAC.
∵2∠BEC﹣∠P=180°,
∴∠BEC![]() ∠P=90°,
∠P=90°,
∴90°![]() ∠P=∠ABC+∠P
∠P=∠ABC+∠P![]() ∠BAC,
∠BAC,
180°+∠P=2∠ABC+2∠P+∠BAC,
180°=∠ABC+∠P+180°﹣∠ACB,
∠ACB=∠ABC+∠P=∠PCD=∠ACP,
∴∠ACB=60°.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】小刚准备用一段长 44 米的篱笆围成三角形,用于养鸡。已知一条边长 x 米,第二条边是第一条边的 3 倍多 6 米。
(1)若能围成一个等腰三角形,求三边长
(2)若第一边长最短,写出 x 的取值范围 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )

A. 赛跑中,兔子共休息了50分钟
B. 乌龟在这次比赛中的平均速度是0.1米/分钟
C. 兔子比乌龟早到达终点10分钟
D. 乌龟追上兔子用了20分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展以“我最喜欢的职业”为主题的调查活动.通过对学生的随机抽样调查得到一组数据,下面两图(如图)是根据这组数据绘制的两幅不完整的统计图.请你根据图中所提供的信息解答下列问题:
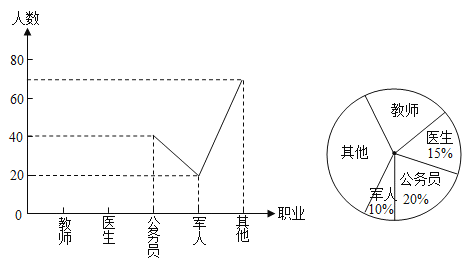
(1)在这次活动中一共调查了 名学生;
(2)在扇形统计图中,求“教师”所在扇形的圆心角的度数;
(3)把折线统计图补充完整;
(4)如果某中学共有2400名学生,请你估计该中学“我最喜欢的职业是教师”的有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】购物广场内甲、乙两家商店对A、B两种商品均有优惠促销活动;
甲商店的促销方案是:A商品打八折,B商品打七五折;
乙商店的促销方案是:购买一件A商品,赠送一件B商品,多买多送。
请你结合小明和小华的对话,解答下列问题:
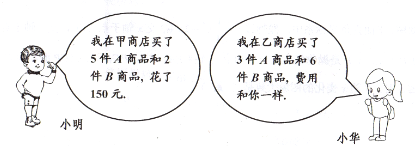
(1)求A、B两种商品促销前的单价;
(2)假设在同一家商店购买A、B两种商品共100件,且A不超过50件,请说明选择哪家商店购买更合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xoy中,抛物线y=a(x+1)(x-9)经过A,B两点,四边形OABC
矩形,已知点A坐标为(0,6)。

(1) 求抛物线解析式;
(2) 点E在线段AC上移动(不与C重合),过点E作EF⊥BE,交x轴于点F.请判断![]() 的值是否变化;若不变,求出它的值;若变化,请说明理由。
的值是否变化;若不变,求出它的值;若变化,请说明理由。
(3)在(2)的条件下,若E在直线AC上移动,当点E关于直线BF的对称点![]() 在抛物线对称轴上时,请求出BE的长度。
在抛物线对称轴上时,请求出BE的长度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ∥
∥![]() ,
,![]() =2
=2![]() ,
,![]() 为
为![]() 的中点,请仅用无刻度的直尺分别按下列要求画图(保留作图痕迹)
的中点,请仅用无刻度的直尺分别按下列要求画图(保留作图痕迹)
(1)在图1中,画出△ABD的BD边上的中线;
(2)在图2中,若BA=BD, 画出△ABD的AD边上的高 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,![]() ,
,![]() ,E是AB上一点,连接CE,现将
,E是AB上一点,连接CE,现将![]() 向上方翻折,折痕为CE,使点B落在点P处.
向上方翻折,折痕为CE,使点B落在点P处.

(1)当点P落在CD上时,![]() _____;当点P在矩形内部时,BE的取值范围是_____.
_____;当点P在矩形内部时,BE的取值范围是_____.
(2)当点E与点A重合时:①画出翻折后的图形(尺规作图,保留作图痕迹);②连接PD,求证:![]() ;
;

(3)如图,当点Р在矩形ABCD的对角线上时,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com