
����Ŀ��һ���ͳ��Ӽؿ����ҵأ�һ��������ҵؿ����أ�����ͬʱ��������ͳ���صľ���Ϊy1ǧ�ף������صľ���Ϊy2ǧ�ף�������ʻ��ʱ��ΪxСʱ��y1��y2����x�ĺ���ͼ����ͼ��ʾ��

��1������ͼ��ֱ��д��y1��y2����x�ĺ�����ϵʽ��
��2����xΪ��ֵʱ������������
��3���ס������ؼ���A��B��������վ�����280ǧ�ף����ͳ�����A����վʱ�����ǡ�ý���B����վ����A����վ��صľ��룮
���𰸡���1��y1��60x��0��x��10����y2����100x+600��0��x��6������2����xΪ![]() Сʱʱ��������������3��A����վ���ؾ���Ϊ120km��330km
Сʱʱ��������������3��A����վ���ؾ���Ϊ120km��330km
��������
��1��ֱ�����ô���ϵ�����Ϳ������y1��y2����x�ĺ���ͼ��ϵʽ��
��2������y1=y2�е�ʽ��������ɣ�
��3����A����վ�ڼ���B����վ֮�䣬B����վ�ڼ���A����վ֮����������г�������⼴�ɣ�
��1����y1��k1x����ͼ��֪������ͼ���㣨10��600����
��10k1��600��
��ã�k1��60��
��y1��60x��0��x��10����
��y2��k2x+b����ͼ��֪������ͼ���㣨0��600������6��0����
��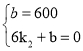 ��
��
��ã�![]() ��
��
��y2����100x+600��0��x��6����
��2�������⣬��
60x����100x+600��
x��![]() ��
��
�𣺵�xΪ![]() hʱ������������
hʱ������������
��3�������⣬��
�ٵ�A����վ�ڼ���B����վ֮��ʱ������100x+600����60x��280��
���x��2��
��ʱ��A����վ����أ�60��2��120km��
�ڵ�B����վ�ڼ���A����վ֮��ʱ��60x������100x+600����280��
���x��5.5����ʱ��A����վ����أ�60��5.5��330km��
����������A����վ���ؾ���Ϊ120km��330km��


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y����![]() x+2��ͼ��x�ᡢy��ֱ��ڵ�A��B����ֱ��y��kx��P��
x+2��ͼ��x�ᡢy��ֱ��ڵ�A��B����ֱ��y��kx��P��
��1�����A��B�����ꣻ
��2����OP��PA����P�����꼰k��ֵ��
��3���ڣ�2���������£�C��ֱ��BP��һ���㣬CE��x����E����ֱ��DP��D����CD��3ED��ֱ��д��C������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���A��50�㣬��B����C����D��E��F�ֱ��ڱ�BC��CA��AB�ϣ�������BF��CD��BD��CE����BFD��30�㣬���FDE�Ķ���Ϊ��������

A.75��B.80��C.65��D.95��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ����BC��AB������OC����AD��OC��ֱ��CD��BA���ӳ����ڵ�E��
��1����֤��ֱ��CD�ǡ�O�����ߣ�
��2����DE��2BC��AD��5����OC��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����������ͬ·��ǰ�����뵥λ10km����ѵ���IJμ�ѧϰ��ͼ��![]() ��
��![]() �ֱ��ʾ�ס�������ǰ��Ŀ�ĵ����ߵ�·��s��ǧ�ף���ʱ��t���֣��仯�ĺ���ͼ������˵�����ټױ�����ǰ12�ֵ���ڼ�ƽ���ٶ�Ϊ15ǧ��/ʱ���ۼ�������ʱ��������6ǧ�ף����ҳ���6���Ӻ��ϼ�.������ȷ���У� ��
�ֱ��ʾ�ס�������ǰ��Ŀ�ĵ����ߵ�·��s��ǧ�ף���ʱ��t���֣��仯�ĺ���ͼ������˵�����ټױ�����ǰ12�ֵ���ڼ�ƽ���ٶ�Ϊ15ǧ��/ʱ���ۼ�������ʱ��������6ǧ�ף����ҳ���6���Ӻ��ϼ�.������ȷ���У� ��
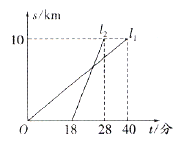
A. 4��B. 3��C. 2��D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�ȱ���ABC��D��AC���е㣬E��BC���ӳ����ϣ���CE��CD����D��DF��BE�ڵ�E��
��������֤����BDEΪ���������Σ�
�����������FC��BF���������ϵ����֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ι��ţ���������ˮ��2mʱ��ˮ���4m����ˮ���½�1mʱ��ˮ���������_____m��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ����x�ᡢy��ֱ���A��B�����߶�ABΪֱ�DZ��ڵ�һ��������Rt��ABC����ʹ��ABC=30����
��ͼ����x�ᡢy��ֱ���A��B�����߶�ABΪֱ�DZ��ڵ�һ��������Rt��ABC����ʹ��ABC=30����
��1����AC�ij��ȣ�
��2������ڵڶ���������һ�� �������ı���AOPB�����S��m֮��ĺ�����ϵʽ��������APB����ABC������ʱm��ֵ��
�������ı���AOPB�����S��m֮��ĺ�����ϵʽ��������APB����ABC������ʱm��ֵ��
��3���Ƿ����ʹ��QAB�ǵ��������β������������ϵĵ�Q�������ڣ���д����Q���п��ܵ����ꣻ�������ڣ���˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ABC�У�D��E�ֱ���AB��AC���ϵĵ㣬��ADC�ա�ADC�䣬��AEB�ա�AEB������C��D��EB���BC��BE��CD���ڵ�F������BAC=35��������BFC�Ĵ�С�ǣ�������

A. 105�� B. 110�� C. 100�� D. 120��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com