
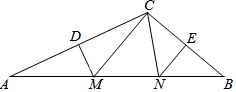
 如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N,
如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N,分析 (1)根据△ABC中,DM、EN分别垂直平分AC和BC,可知AM=CM,CN=BN,可知△CMN的周长即为AB的长.
(2)根据垂直平分线的性质可知,∠1=∠2,∠3=∠4,根据三角形的内角和定理,整体求出∠1+∠4的值,进而可得∠ACB的度数.
解答 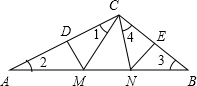 解:(1)∵DM、EN分别垂直平分AC和BC,
解:(1)∵DM、EN分别垂直平分AC和BC,
∴AM=CM,CN=BN,
∵△CMN的周长为18cm,即CM+CN+MN=18,
∴AM+BN+MN=AB=18cm.
∴AB=18cm.
(2)∵DM垂直平分AC,
∴∠1=∠2,
∵EN垂直平分BC,
∴∠3=∠4,
又∵∠1+∠2+∠3+∠4+50°=180°,
则2(∠1+∠4)=180°-50°=130°,
∠1+∠4═65°,
∴∠ACB=(∠1+∠4)+∠MCN=65°+50°=115°.
点评 此题主要考查线段的垂直平分线的性质等几何知识,由线段的垂直平分线上的点到线段的两个端点的距离相等,可得到等腰三角形△AMC、△CNB,再利用等腰三角形的两底角相等,得到∠1=∠2,∠3=∠4,再根据三角形的内角和等于180°求出∠1+∠4,便可解答.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 填写理由:
填写理由:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
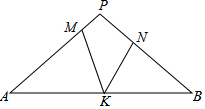 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )| A. | 44° | B. | 66° | C. | 96° | D. | 92° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com