
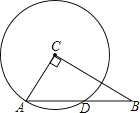
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】钓鱼岛是我国渤海海峡上的一颗明珠,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向钓鱼岛驶来,渔船向渔政部门报告,并立即返航.渔政船接到报告后,立即从该港口出发赶往钓鱼岛.下图是渔船及渔政船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)

(1)直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.]
(2)求渔船和渔政船相遇时,两船与钓鱼岛的距离.
(3)在渔政船驶往钓鱼岛的过程中,求渔船从港口出发经过多长时间与渔政船相距30海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,已知A(3,4),B(3,﹣1),C(﹣3,﹣2),D(﹣2,3)
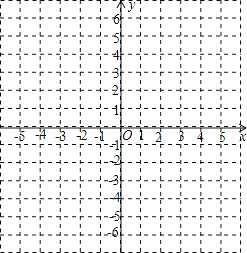
(1)在图上画出四边形ABCD,并求四边形ABCD的面积;
(2)若P为四边形ABCD形内一点,已知P坐标为(﹣1,1),将四边形ABCD通过平移后,P的坐标变为(2,﹣2),根据平移的规则,请直接写出四边形ABCD平移后的四个顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米.
(1)请用代数式表示A、B两园区的面积之和并化简;
(2)现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米,整改后A区的长比宽多350米,且整改后两园区的周长之和为980米.
①求x、y的值;
②若A园区全部种植C种花,B园区全部种植D种花,且C、D两种花投入的费用与吸引游客的收益如表:

求整改后A、B两园区旅游的净收益之和.(净收益=收益﹣投入)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一副三角板的两个直角顶点重合在一起.
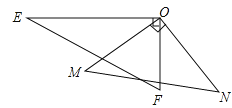
(1)若∠EON=140°,求∠MOF的度数;
(2)比较∠EOM与∠FON的大小,并写出理由;
(3)求∠EON+∠MOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,P是∠ABC内一点,请过点P画射线PD,使PD∥BC;过点P画直线PE∥BA,交BC于点E.请画图并通过观察思考后你发现∠ABC与∠DPE的大小关系是 ,并说明理由.
(2)如图2,直线a,b所成的角跑到画板外面去了,为了测量这两条直线所成的角的度数,请画图并简单地写出你的方法.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com