
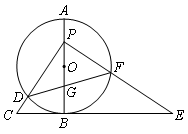
 ;(2)2或
;(2)2或 .
. ,在Rt△PBE中,由勾股定理可求得PE的长;(2)分弦DF不是直径和弦DF恰为直径两种情况讨论即可.
,在Rt△PBE中,由勾股定理可求得PE的长;(2)分弦DF不是直径和弦DF恰为直径两种情况讨论即可. ,∴
,∴ .
. .
. ×2×2=2.
×2×2=2. ×10×4=20,∴由△PCE∽△PFD得,S△PDF=
×10×4=20,∴由△PCE∽△PFD得,S△PDF= .
.


科目:初中数学 来源:不详 题型:解答题

 对称的△A1B1C1,并写出点C1 的坐标;
对称的△A1B1C1,并写出点C1 的坐标; )
)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ;
;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com