
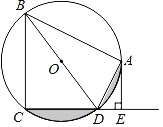
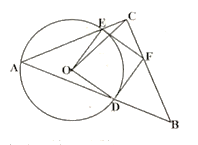
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,AD平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)如果AB=6,AE=3,求:阴影部分面积.
【答案】(1)见解析 (2)![]()
【解析】
(1)连接OA,利用已知首先得出OA∥DE,进而证明OA⊥AE就能得到AE是⊙O的切线;
(2)通过证明△BAD∽△AED,再利用对应边成比例关系从而求出⊙O半径的长,解直角三角形即可得到结论.
(1)证明:连接OA,
∵OA=OD,
∴∠1=∠2.
∵DA平分∠BDE,
∴∠2=∠3.
∴∠1=∠3.
∴OA∥DE.
∴∠OAE+∠AED=180°,
∵AE⊥CD,
∴![]()
∴∠OAE=90°,
即OA⊥AE.
又∵点A在⊙O上,
∴AE是⊙O的切线;
(2)解:∵BD是⊙O的直径,
∴∠BAD=90°.
∵∠AED=90°,
∴∠BAD=∠AED,
又∵∠2=∠3,
∴![]() .
.
∴![]()
∵BA=6,AE=3,
∴BD=2AD,
∴∠ABD=30°,
![]()
由![]()
∴BD=![]() ,
,
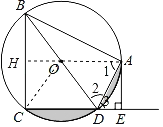
延长AO交BC于H,
则四边形AHCE是矩形,
∴∠AHC=90°,CH=AE=3,
∴BC=2CH=6,
∴cos∠CBD=![]()
∴∠CBD=30°,
∴∠COD=∠AOD=60°,![]()
由阴影部分面积=![]()
∴阴影部分面积=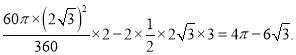


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于A,B两点(点A在点B左侧)
轴交于A,B两点(点A在点B左侧)
(1)求抛物线的顶点坐标(用含![]() 的代数式表示);
的代数式表示);
(2)求线段AB的长;
(3)抛物线与![]() 轴交于点C(点C不与原点
轴交于点C(点C不与原点![]() 重合),若
重合),若![]() 的面积始终小于
的面积始终小于![]() 的面积,求
的面积,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数解析式为y=mx2﹣2mx+m﹣![]() ,二次函数与x轴交于A、B两点(B在A右侧),与y轴交于C点,二次函数顶点为M.已知∠OMB=90°.
,二次函数与x轴交于A、B两点(B在A右侧),与y轴交于C点,二次函数顶点为M.已知∠OMB=90°.
①求顶点坐标.
②求二次函数解析式.
③N为线段BM中点,在二次函数的对称轴上是否存在一点P,使得∠PON=60°,若存在求出点P坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰![]() 的一个锐角顶点
的一个锐角顶点![]() 是
是![]() 上的一个动点,
上的一个动点,![]() ,腰
,腰![]() 与斜边
与斜边![]() 分别交
分别交![]() 于点
于点![]() ,分别过点
,分别过点![]() 作
作![]() 的切线交于点
的切线交于点![]() ,且点
,且点![]() 恰好是腰
恰好是腰![]() 上的点,连接
上的点,连接![]() ,若
,若![]() 的半径为4,则
的半径为4,则![]() 的最大值为:( )
的最大值为:( )
A.![]() B.
B.![]() C.6D.8
C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正确结论有( )
.其中正确结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
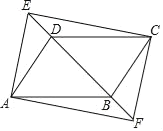
【题目】如图,在ABCD中,点E,F是直线BD上的两点,DE=BF.
(1)求证:四边形AFCE是平行四边形.
(2)若BD⊥AD,AB=5,AD=3,四边形AFCE是矩形,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
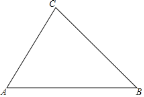
【题目】如图,已知△ABC,请用直尺(不带刻度),和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹).
(1)作菱形AMNP,使点M,N、P在边AB、BC、CA上;
(2)当∠A=60°,AB=4,AC=3时,求菱形AMNP的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com