
 据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪.如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°
据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪.如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°分析 (1)在Rt△ABD中求出BD,在Rt△ACD中求出CD,根据BC=BD-CD计算即可;
(2)求出 轿车的速度与15m/s比较即可判断;
解答 解:(1)在Rt△ABD中,AD=24m,∠B=31°,
∴tan31°=$\frac{AD}{BD}$,即BD=$\frac{24}{0.6}$=40m,
在Rt△ACD中,AD=24m,∠ACD=50°,
∴tan50°=$\frac{AD}{CD}$,即CD=$\frac{24}{1.2}$=20m,
∴BC=BD-CD=40-20=20m,
则B,C的距离为20m;
(2)根据题意得:20÷2=10m/s<15m/s,
则此轿车没有超速.
点评 本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是熟练掌握锐角三角函数的定义,属于中考常考题型.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:选择题
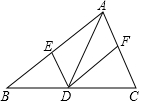 在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )| A. | 若AD⊥BC,则四边形AEDF是矩形 | |
| B. | 若AD垂直平分BC,则四边形AEDF是矩形 | |
| C. | 若BD=CD,则四边形AEDF是菱形 | |
| D. | 若AD平分∠BAC,则四边形AEDF是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 公路施工中需要建设穿过小山的隧道DE,采用从两边同时施工的方法,甲工程队从D向E施工,乙工程队从E向D施工,为了使两工程队施工能在山中对接,需要保证A,D,E,C,在同一直线上.为此,在
公路施工中需要建设穿过小山的隧道DE,采用从两边同时施工的方法,甲工程队从D向E施工,乙工程队从E向D施工,为了使两工程队施工能在山中对接,需要保证A,D,E,C,在同一直线上.为此,在查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com