
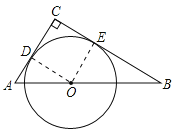
【题目】如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.

(1)当AC=2时,求⊙O的半径;
(2)设AC=x,⊙O的半径为y,求y与x的函数关系式.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)连接OD,OE,先证四边形OECD是正方形,在△ADO中,解直角三角形即可得到半径.
(2)由题意可知,OD∥BC,∠AOD=∠B,则两角正切值相等,进而列出关系式.
试题解析:(1)连接OE,OD,在△ABC中,∠C=90°,AC+BC=8,∵AC=2,∴BC=6,∵以O为圆心的⊙O分别与AC,BC相切于点D,E,∴四边形OECD是正方形,tan∠B=tan∠AOD=![]() =
=![]() ,解得OD=
,解得OD=![]() ,∴圆的半径为
,∴圆的半径为![]() ;
;
(2)∵AC=x,BC=8﹣x,在直角三角形ABC中,tanB=![]() ,∵以O为圆心的⊙O分别与AC,BC相切于点D,E,∴四边形OECD是正方形,tan∠AOD=tanB=
,∵以O为圆心的⊙O分别与AC,BC相切于点D,E,∴四边形OECD是正方形,tan∠AOD=tanB=![]() =
=![]() ,解得
,解得![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,己知O为坐标原点,点A(3,0),B(0.4),以点A为旋转中心,把△ABO顺时针旋转,得△ACD.记旋转角为α.∠ABO为β.

(I )如图①,当旋转后点D恰好落在AB边上时,求点D的坐标;
(II)如图②,当旋转后满足BC∥x轴时,求α与β之间的数量关系:
(III)当旋转后满足∠AOD=β时,求直线CD的解析式(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
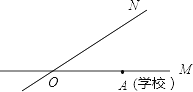
【题目】如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音影响,已知有两台相距30米的拖拉机正沿ON方向行驶,它们的速度均为5米/秒,问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,正方形ABCD中,AD=4,点E在CD上,DE=3CE,F是AD上异于D的点,且∠EFB=∠FBC,则tan∠DFE=( )

A. 2![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P,根据下列条件,求∠BPC的度数.
(1)若∠ABC=50°,∠ACB=60°,则∠BPC= ;
(2)若∠ABC+∠ACB=120°,则∠BPC= ;
(3)若∠A=80°,则∠BPC= ;
(4)从以上的计算中,你能发现已知∠A,求∠BPC的公式是:∠BPC= (提示:用∠A表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在线段AB上有一点C(点C不与A、B重合且AC>BC),分别以AC、BC为边作正方形ACED和正方形BCFG,其中点F在边CE上,连接AG.

(1)如图1,若AC=7,BC=5,则AG=______;
(2)如图2,若点C是线段AB的三等分点,连接AE、EG,求证:△AEG是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知正方形ABCO,A(0,3),点D为x轴上一动点,以AD为边在AD的右侧作等腰Rt△ADE,∠ADE=90°,连接OE,则OE的最小值为( )

A. ![]() B.
B. ![]() C. 2
C. 2![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由边长为1个单位长度的小正方形组成的网格图中有格点△ABC.
(注:顶点在网格线交点处的三角形叫做格点三角形)
(1)图中AB的长为_________个单位长度;
(2)只用没有刻度的直尺,按如下要求画图:
① 以点C为位似中心,作△DEC∽△ABC,且相似比为1∶2;
②若点B为原点,点A(1,3),请在图2中画出平面直角坐标系,直接出△ABC的外心的坐标______________

查看答案和解析>>
科目:初中数学 来源: 题型:
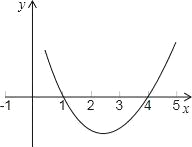
【题目】已知,二次函数y=ax2﹣5x+c的图象如图.
(1)求这个二次函数的解析式和它的图象的顶点坐标;
(2)观察图象,回答:何时y随x的增大而增大;何时y随x的增大而减小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com