
分析 根据“两点之间,线段最短”来解答问题:作出点B关于x轴的对称点B′,过B′作B′M⊥x轴,M是垂足,连结AB′,交x轴于点P,即点A、P、B′共线时,PA+PB的值最小.
解答 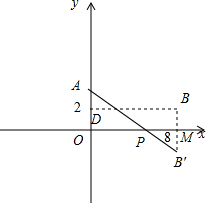 解:如图,作出点B关于x轴的对称点B′,过B′作B′M⊥x轴,M是垂足,连结AB′,交x轴于点P.
解:如图,作出点B关于x轴的对称点B′,过B′作B′M⊥x轴,M是垂足,连结AB′,交x轴于点P.
∵点B关于x轴的对称点是B′,∴PB=PB′,
∴AB′=AP+PB′=AP+PB,
而A、B′两点间线段最短,
∴AB′最短,(两点之间,线段最短),即AP+PB最小,
∴在Rt△AMB′中,AM=3,MB′=8,
∴AB′=10.
即PA+PB的最小值为10.
故答案是:10.
点评 此题主要考查了轴对称最短路线问题,求两线段之和最小的基本方法是作其中一个已知点关于直线的对称点,从而将两条线段之和转化为另一个已知点与对称点之间的线段.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com