
某物流公司的快递车和货车每天往返于甲、乙两地,快递车比货车多往返一趟.
已知货车比快递车早1小时出发,到达乙地后用1小时装卸货物,然后按原路以原速返回,
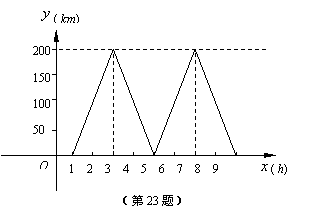
结果与第二趟返回的快递车同时到达甲地.下图表示快递车距离甲地的路程y(km)与货
车出发所用时间x(h)之间的函数关系图象.
(1)①请在下图中画出货车距离甲地的路程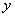 (km)与所用时间
(km)与所用时间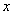 ( h)的函数关系图象;
( h)的函数关系图象;
②两车在中途相遇 次.
(2)试求货车从乙地返回甲地时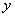 (km)与所用时间
(km)与所用时间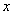 ( h)的函数关系式.
( h)的函数关系式.
(3)求快递车第二次从甲地出发到与返程货车相遇所用时间为多少h?这时货车离
乙地多少km?
 |
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
魏县鸭梨是我省的特产,经过加工后出售,单价可能提高20%,但重量会减少10%。现有未加工的鸭梨30千克,加工后可以比不加工多卖12元,设加工前每千克卖x元,加工后每千克卖y元,根据题意,可列方程组________
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,平行四边形ABCD中,M,N分别是AB,CD的中点,将四边形MBCN沿直线MN折叠后得到四边形MB′C′N,MB′与DN交于点P.若∠A=64°,则∠MPN= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点 在线段
在线段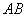 上,
上,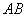 =8,
=8, =2,
=2,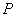 为线段
为线段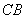 上一动点,点
上一动点,点 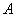 绕点
绕点 旋转后与点
旋转后与点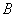 绕点
绕点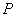 旋转 后重合于点
旋转 后重合于点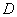 .设
.设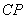 =
=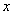 ,
,
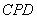 的面积为
的面积为 . 则下列图象中,能表示与
. 则下列图象中,能表示与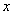 的函数关系的图象大致是
的函数关系的图象大致是
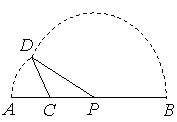
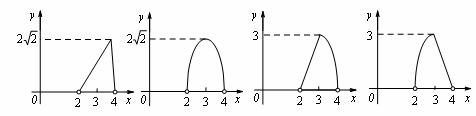
A. B. C. D.
查看答案和解析>>
科目:初中数学 来源: 题型:
定义:如果一个 与
与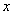 的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是
的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是 与
与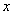 的“反比例平移函数”.
的“反比例平移函数”.
例如: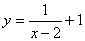 的图象向左平移2个单位,再向下平移1个单位得到
的图象向左平移2个单位,再向下平移1个单位得到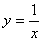 的图象,则
的图象,则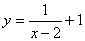 是
是 与
与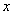 的“反比例平移函数”.
的“反比例平移函数”.
(1)若矩形的两边分别是2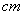 、3
、3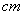 ,当这两边分别增加
,当这两边分别增加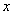 (
(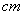 )、
)、 (
(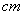 )后,得到的新矩形的面积为8
)后,得到的新矩形的面积为8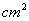 ,求
,求 与
与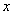 的函数表达式,并判断这个函数是否为“反比例平移函数”.
的函数表达式,并判断这个函数是否为“反比例平移函数”.
(2)如图,在平面直角坐标系中,点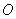 为原点,矩形
为原点,矩形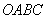 的顶点
的顶点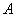 、
、 的坐标分别为(9,0)、(0,3) .点
的坐标分别为(9,0)、(0,3) .点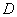 是
是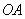 的中点,连接
的中点,连接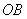 、
、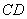 交于点
交于点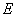 ,“反比例平移函数”
,“反比例平移函数”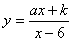 的图象经过
的图象经过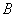 、
、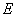 两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
( 3)在(2)的条件下, 已知过线段
3)在(2)的条件下, 已知过线段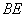 中点的一条直线
中点的一条直线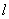 交这个“反
交这个“反
比例平移函数”图象于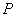 、
、 两点(
两点(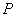 在
在 的右侧),若
的右侧),若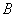 、
、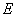 、
、
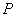 、
、 为顶点组成的四边形面积为16,请求出点
为顶点组成的四边形面积为16,请求出点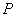 的坐标.
的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com