
 有一座抛物线形拱桥,正常水位时,桥下水面宽20m,拱顶距离水面4m.
有一座抛物线形拱桥,正常水位时,桥下水面宽20m,拱顶距离水面4m.分析 (1)如图1,根据已知表示出点B的坐标,利用待定系数法求抛物线的解析式;
(2)如图2,表示出点E的坐标($\frac{d}{2}$,h-4),注意其纵坐标为负数,代入抛物线的解析式即可;
(3)根据水面的宽度不得小于18m,可知抛物线上一点的横坐标大于9时,符合题意,因此将x=9代入,求出y=-3.24,即这时的水深为4-3.24+2=2.76米,得出结论.
解答 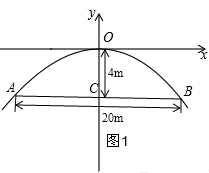 解:(1)如图1,设抛物线的解析式为:y=ax2;
解:(1)如图1,设抛物线的解析式为:y=ax2;
由题意得:B(10,-4),
把B(10,-4)代入y=ax2得:100a=-4,
a=-$\frac{1}{25}$,
∴该抛物线的解析式为:y=-$\frac{1}{25}$x2;
(2)如图2,由题意得:E($\frac{d}{2}$,h-4),
把E($\frac{d}{2}$,h-4)代入y=-$\frac{1}{25}$x2得:-$\frac{1}{25}$×$(\frac{d}{2})^{2}$=h-4,
h=-$\frac{1}{100}$d2+4,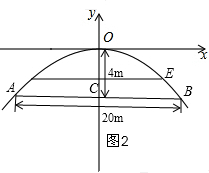
所以用d表示h的函数解析式为:h=-$\frac{1}{100}$d2+4;
(3)当x=9时,y=-$\frac{1}{25}$×92=-3.24,
4-3.24+2=2.76,
答:当水深超过2.76米时,会影响过往船只在桥下通行.
点评 本题考查了二次函数的实际应用,属于隧道问题;此类问题要建立恰当的平面直角坐标系,先求出抛物线的解析式,运用已知条件表示出相应点的坐标,在解题时注意点的坐标特点和线段的长.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
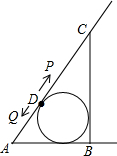 如图,△ABC中,CB=8,AB=6,AC=10,△ABC的内切圆交 AC于点D,点P从D出发,沿射线DC每次前进一个单位,点Q从D出发沿DA和射线AB每次前进a个单位,a为正整数且1≤a<5,当t次前进后△APQ与△ABC相似,所有满足条件的t为8、16、32.
如图,△ABC中,CB=8,AB=6,AC=10,△ABC的内切圆交 AC于点D,点P从D出发,沿射线DC每次前进一个单位,点Q从D出发沿DA和射线AB每次前进a个单位,a为正整数且1≤a<5,当t次前进后△APQ与△ABC相似,所有满足条件的t为8、16、32.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
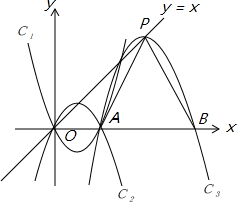 已知抛物线C1的解析式为y=(x-1)2-1,将C1沿x轴翻折得抛物线C2.
已知抛物线C1的解析式为y=(x-1)2-1,将C1沿x轴翻折得抛物线C2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com