
【题目】对于平面直角坐标系 ![]() 中的点
中的点![]() ,给出如下定义:记点
,给出如下定义:记点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,到
,到![]() 轴的距离为
轴的距离为![]() 若
若![]() ≤
≤![]() ,则称
,则称![]() 为点
为点![]() 的“引力值”;若
的“引力值”;若![]() ,则称
,则称![]() 为点
为点![]() 的“引力值”.特别地,若点
的“引力值”.特别地,若点![]() 在坐标轴上,则点
在坐标轴上,则点![]() 的“引力值”为0.
的“引力值”为0.
例如,点P(-2,3)到![]() 轴的距离为3 ,到
轴的距离为3 ,到![]() 轴的距离为2 ,因为2<3,所以点
轴的距离为2 ,因为2<3,所以点![]() 的“引力值”为2.
的“引力值”为2.
(1)①点![]() 的“引力值”为 ;②若点
的“引力值”为 ;②若点![]() 的“引力值”为2,则
的“引力值”为2,则![]() 的值为 ;
的值为 ;
(2)若点C在直线![]() 上,且点C的:“引力值”为2,求点C的坐标;
上,且点C的:“引力值”为2,求点C的坐标;
(3)已知点M是以D(3,4)为圆心,半径为2的圆上的一个动点,那么点M的“引力值”![]() 的取值范围是
的取值范围是
【答案】(1)①1, ②![]() ;(2) 点C的坐标为(-2,8)或(3,-2);(3)
;(2) 点C的坐标为(-2,8)或(3,-2);(3) ![]()
【解析】试题分析:(1)根据“引力值”的定义进行解答即可;
(2)设出C点坐标,由C在直线![]() 上,且“引力值”为2,可分情况讨论;
上,且“引力值”为2,可分情况讨论;
(3)在圆上找到和两坐标轴最近和最远的点,比较即可.
试题解析:(1)①点![]() 到
到![]() 轴的距离为4 ,到
轴的距离为4 ,到![]() 轴的距离为1,因为1<4,所以点
轴的距离为1,因为1<4,所以点![]() 的“引力值”为1;
的“引力值”为1;
②点![]() 的“引力值”为2,则
的“引力值”为2,则![]() ,a
,a![]() ;
;
(2)设点C的坐标为(![]() ).
).
由于点C的“引力值|”为2,则![]() 或
或![]() ,即
,即![]() ,或
,或![]() ,
,
当![]() 时,
时, ![]() ,此时点C的“引力值”为0,舍去;
,此时点C的“引力值”为0,舍去;
当![]() 时,
时, ![]() 此时C点坐标为(-2,8);
此时C点坐标为(-2,8);
当![]() 时,
时, ![]() 解得
解得![]() ,此时点C的“引力值”1,舍去;
,此时点C的“引力值”1,舍去;
当![]() 时,
时, ![]() ,
, ![]() ,此时C点坐标为(3,-2);
,此时C点坐标为(3,-2);
综上所述,点C的坐标为(-2,8)或(3,-2).
(3)以D(3,4)为圆心,半径为2的圆上的点中,距离x轴最近和最远的点分别为(3,2),(3,6),距离y轴最近和最远的点分别为(1,4),(5,4),所以点M的“引力值”![]() 的取值范围是1≤d≤6.
的取值范围是1≤d≤6.


科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A.某种彩票的中奖率为1%,买100张彩票一定有1张中奖
B.从装有10个红球的袋子中,摸出1个白球是不可能事件
C.为了解一批日光灯的使用寿命,可采用抽样调查的方式
D.掷一枚普通的正六面体骰子,出现向上一面点数是2的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将7张如图①所示的长为a、宽为b(a>b)的小长方形纸片,按如图②所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设左上角与右下角的阴影部分的面积之差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a、b应满足( )
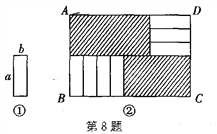
A. a=![]() b B. a=3b C. a=
b B. a=3b C. a=![]() b D. a=4b
b D. a=4b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线C:y=x2-4x+4和直线l:y=kx-2k(k>0).
(1)抛物线C的顶点D的坐标为 ;
(2)请判断点D是否在直线![]() 上,并说明理由;
上,并说明理由;
(3)记函数![]() 的图像为G,点M(0,t),过点M垂直于
的图像为G,点M(0,t),过点M垂直于![]() 轴的直线与图像G交于点
轴的直线与图像G交于点![]() .当1<t<3时,若存在t使得
.当1<t<3时,若存在t使得![]() 成立,结合图像,求k的取值范围.
成立,结合图像,求k的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A坐标为(6,0),点B在y轴的正半轴上,且![]() =240.
=240.
(1)求点B坐标;
(2)若点P从B出发沿y轴负半轴方向运动,速度每秒2个单位,运动时间t秒,△AOP的面积为S,求S与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,若S△AOP:S△ABP=1:3,且S△AOP+S△ABP=S△AOB,在线段AB的垂直平分线上是否存在点Q,使得△AOQ的面积与△BPQ的面积相等?若存在,求出Q点坐标;若不存在,请说明理由。



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.在同一平面内,两条直线的位置只有平行和垂直两种
B.两直线平行,同旁内角相等
C.过一点有且只有一条直线与已知直线平行
D.平行于同一条直线的两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图所示,已知∠1 = ∠2,∠B = ∠C,可推得AB∥CD,

理由如下:
∵∠1 = ∠2(已知),且∠1 = ∠4(_____________________),
∴∠2 = ∠4(等量代换).
∴CE∥BF(__________________________).
∴∠_____= ∠3(________________________)
又∵∠B = ∠C(已知),
∴∠3= ∠B(等量代换),
∴AB∥CD(_____________________________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com