
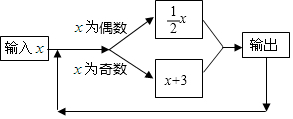
分析 (1)根据数值转换机的运算程序,以及有理数的混合运算的运算方法,求出第1次输入的数为2时,第2次输出的数为多少,以及第1次输入的数为12时,第5次输出的数为多少即可.
(2)根据数值转换机的运算程序,以及有理数的混合运算的运算方法,求出若输入的数为5,每次输出的数的规律,判断出第2016次输出的数是多少即可.
(3)根据数值转换机的运算程序,求出所有x的值,使得输入的数和第3次输出的数相等即可.
解答 解:(1)∵1+3=4,
∴第1次输出的数为1,则第2次输出的数为4.
12×$\frac{1}{2}$=6,6×$\frac{1}{2}$=3,3+3=6,6×$\frac{1}{2}$=3,3+3=6,
∴第1次输入的数为12,则第5次输出的数为6.
(2)5+3=8,8×$\frac{1}{2}$=4,4×$\frac{1}{2}$=2,2×$\frac{1}{2}$=1,1+3=4,
∴若输入的数为5,则每次输出的数分别是8、4、2、1、4、2、1,…,
(2016-1)÷3
=2015÷3
=671…2
∴第2016次输出的数是2.
(3)如图,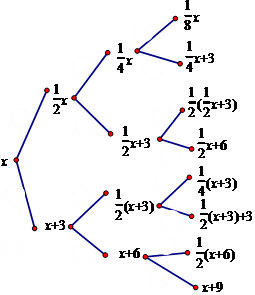 ,
,
由x=$\frac{1}{8}$x,解得x=0;符合题意;
由x=$\frac{1}{4}$x+3,解得x=4;符合题意,
由x=$\frac{1}{2}$($\frac{1}{2}$x+3),解得x=2;符合题意,
由x=$\frac{1}{2}$x+6,解得x=12;$\frac{1}{2}$x=6,偶数,不符合题意;
由x=$\frac{1}{4}$(x+3),解得x=1;符合题意;
由x=$\frac{1}{2}$(x+3)+3,解得x=9;x+3=12,是偶数,不符合题意,
由x=$\frac{1}{2}$(x+6),解得x=6;而x是偶数,不符合题意;
由x=x+9,解得x无解;
∴存在输入的数x,使第3次输出的数是x,此时x=0,1,2,4;
故答案为:4、6.
点评 此题主要考查了代数式求值问题,要熟练掌握,求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
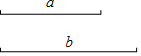 已知:线段a,b.
已知:线段a,b.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
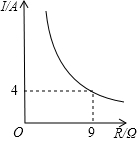 已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com