
| 分数段/分 | 组中值 | 频数(人数) | 频率 |
| 60≤x<70 | 65 | 30 | 0.15 |
| 70≤x<80 | 75 | b | 0.45 |
| 80≤x<90 | 85 | 60 | c |
| 90≤x<100 | a | 20 | 0.1 |
分析 (1)a=(90+100)×$\frac{1}{2}$,求出总人数,再根据b=总人数×0.45,c=60÷总人数计算即可;
(2)根据共有200个数,得出中位数是第100、101个数的平均数,根据加权平均数的计算公式列式计算即可;
(3)用比赛成绩80分以上(含80分)的人数除以总人数即可得出获奖率.
解答 解:(1)表中a=(90+100)×$\frac{1}{2}$=95,
∵总人数是30÷0.15=200,
∴b=200×0.45=90,
c=60÷200=0.3,
故答案为:95,90,0.3;
(2)∵共有200个数,
∴中位数是第100、101个数的平均数,
∴参赛学生比赛成绩的中位数落在70≤x<80这个分数段,
参赛学生成绩的平均得分=(65×30+75×90+85×60+95×20)÷200=78.5;
(3)如果比赛成绩80分以上(含80分)可获得奖励,那么获奖率是$\frac{60+20}{200}$×100%=40%.
点评 本题考查了中位数、平均数,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
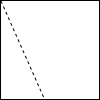 如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )| A. | 直角三角形 | B. | 平行四边形 | C. | 菱形 | D. | 等腰梯形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在?ABCD中,AB=2BC=4,E、F分别为AB、CD的中点
在?ABCD中,AB=2BC=4,E、F分别为AB、CD的中点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD是矩形纸片,AD=10,CD=8,在CD上取一点E,将纸片沿AE翻折,使点D落在BC边上的点F处.
如图,四边形ABCD是矩形纸片,AD=10,CD=8,在CD上取一点E,将纸片沿AE翻折,使点D落在BC边上的点F处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com