
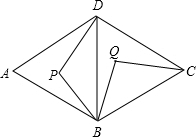
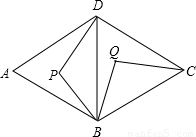
 如图:菱形ABCD是由两个正三角形拼成的,点P在△ABD内任一点,现把△BPD绕点B旋转到△BQC的位置.则
如图:菱形ABCD是由两个正三角形拼成的,点P在△ABD内任一点,现把△BPD绕点B旋转到△BQC的位置.则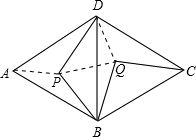 解:(1)连接DQ,当四边形BPDQ是平行四边形时,BQ=PD,
解:(1)连接DQ,当四边形BPDQ是平行四边形时,BQ=PD,| 1 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
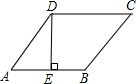 如图,菱形ABCD是周长为20cm,DE⊥AB,垂足为E,cosA=
如图,菱形ABCD是周长为20cm,DE⊥AB,垂足为E,cosA=| 4 |
| 5 |
| A、4个 | B、3个 | C、2个 | D、1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:菱形ABCD是由两个正三角形拼成的,点P在△ABD内任一点,现把△BPD绕点B旋转到△BQC的位置.则
如图:菱形ABCD是由两个正三角形拼成的,点P在△ABD内任一点,现把△BPD绕点B旋转到△BQC的位置.则查看答案和解析>>
科目:初中数学 来源:2010年理科实验班招生数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年浙江省杭州市拱墅区中考数学二模试卷(解析版) 题型:选择题
 ,则下列结论中:①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2;④对角线AC=1.5BD.正确的个数为( )
,则下列结论中:①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2;④对角线AC=1.5BD.正确的个数为( )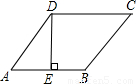
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com