
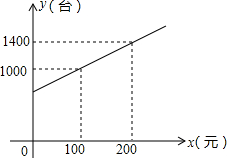
 为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益p(元)会相应降低且满足:p=-$\frac{1}{5}$x+110(x≥0).
为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益p(元)会相应降低且满足:p=-$\frac{1}{5}$x+110(x≥0).分析 (1)根据题意,可设y=kx+b,将(100,1000),(200,1400)代入上式,即可解决问题.
(2)分别求出销售台数,每台的利润,即可解决问题.
(3)构建二次函数,然后利用配方法确定函数最值问题.
解答 解:(1)根据题意,可设y=kx+b
将(100,1000),(200,1400)代入上式,得:$\left\{\begin{array}{l}100k+b=1000\\ 200k+b=1400\end{array}\right.$,
解得$\left\{\begin{array}{l}k=4\\ b=600\end{array}\right.$,
故所求作的函数关系式为:y=4x+600.
(2)∵在y=4x+600中,当x=0时,y=600,
在$p=-\frac{1}{5}x+110$中,当x=0时,p=110
∴600×110=66000
答:在政府未出台补贴措施之前,该商场销售彩电的总收益额为66000元.
(3)设总收益为W元,则
W=$(4x+600)(-\frac{1}{5}x+110)$
=$-\frac{4}{5}{x^2}+320x+66000$
=$-\frac{4}{5}{(x-200)^2}+98000$
∵$a=-\frac{4}{5}<0$,
∴W存在最大值,
∴当x=200时W有最大值98000.
答:政府应将每台补贴款额定为200元时,可获得最大利润98000元.
点评 本题考查二次函数的应用,解题的关键是搞清楚销售量、利润、销售数量之间的关系,学会构建二次函数解决最值问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
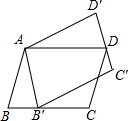 如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )
如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )| A. | 105° | B. | 150° | C. | 75° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
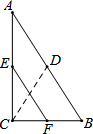 如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,则DC和EF的大小关系是( )
如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,则DC和EF的大小关系是( )| A. | DC>EF | B. | DC<EF | C. | DC=EF | D. | 无法比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+1=0 | B. | x2+4x+4=0 | C. | x2+x+(-$\frac{1}{2}$)=0 | D. | x2-x+$\frac{1}{2}$=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com